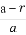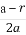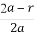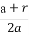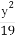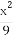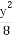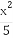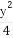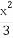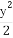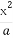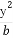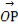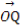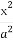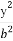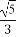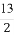题目内容
已知椭圆C: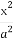 +
+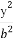 =1(a>b>0)的右焦点为F(1,0),且点(-1,
=1(a>b>0)的右焦点为F(1,0),且点(-1,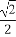 )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的标准方程.
(2)已知点Q( ,0),动直线l过点F,且直线l与椭圆C交于A,B两点,证明:
,0),动直线l过点F,且直线l与椭圆C交于A,B两点,证明: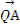 ·
·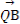 为定值.
为定值.
(1)  +y2=1 (2)见解析
+y2=1 (2)见解析
【解析】(1)由题意知:c=1.
根据椭圆的定义得:2a=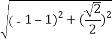 +
+ ,
,
即a=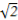 ,所以b2=2-1=1,
,所以b2=2-1=1,
所以椭圆C的标准方程为 +y2=1.
+y2=1.
(2)当直线l的斜率为0时,A(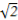 ,0),B(-
,0),B(-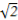 ,0),
,0),
则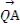 ·
·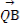 =(
=(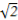 -
-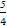 ,0)·(-
,0)·(-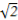 -
-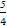 ,0)=-
,0)=-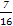 .
.
当直线l的斜率不为0时,设直线l的方程为
x=ty+1,A(x1,y1),B(x2,y2).
由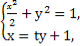 可得(t2+2)y2+2ty-1=0.
可得(t2+2)y2+2ty-1=0.
显然Δ>0.所以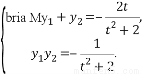
因为x1=ty1+1,x2=ty2+1,
所以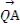 ·
·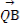 =(x1-
=(x1-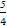 ,y1)·(x2-
,y1)·(x2-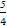 ,y2)
,y2)
=(ty1-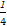 )(ty2-
)(ty2-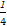 )+y1y2
)+y1y2
=(t2+1)y1y2-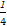 t(y1+y2)+
t(y1+y2)+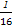
=-(t2+1)·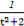 +
+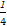 t·
t·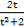 +
+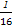
=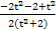 +
+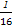 =-
=-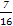 .
.
即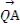 ·
·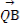 =-
=-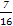 ,为定值.
,为定值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目