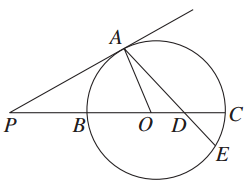
题目内容
设F1,F2分别为双曲线
-
=1的左右焦点,过F1引圆x2+y2=9的切线F1P交双曲线的右支于点P,T为切点,M为线段F1P的中点,O为坐标原点,则|MO|-|MT|等于( )
| x2 |
| 9 |
| y2 |
| 16 |
| A.4 | B.3 | C.2 | D.1 |
∵MO是△PF1F2的中位线,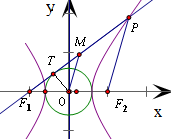
∴|MO|=
|PF2|,|MT|=
|PF1|-|F1T|,
根据双曲线的方程得:
a=3,b=4,c=
=5,∴|OF1|=5,
∵PF1是圆x2+y2=9的切线,|OT|=3,
∴Rt△OTF1中,|FT|=
=4,
∴|MO|-|MT|=|=
|PF2|-(
|PF1|-|F1T|)=|F1T|-
(|PF1|-|PF2|)=4-a=1
故选:D

∴|MO|=
| 1 |
| 2 |
| 1 |
| 2 |
根据双曲线的方程得:
a=3,b=4,c=
| a2+b2 |
∵PF1是圆x2+y2=9的切线,|OT|=3,
∴Rt△OTF1中,|FT|=
| 52-32 |
∴|MO|-|MT|=|=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:D

练习册系列答案
相关题目
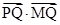 的最小值;
的最小值;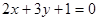 和圆
和圆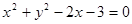 相交于点
相交于点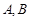 ,则弦
,则弦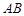 的垂直平分线的方程是_________.
的垂直平分线的方程是_________.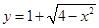
 与直线
与直线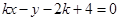 有两个相异的交点时,实数k的取值范围是( )
有两个相异的交点时,实数k的取值范围是( )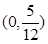
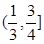
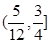
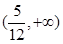
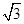 ,∠APB=30°,则AE=________.
,∠APB=30°,则AE=________.