题目内容
已知定点F(1,0),动点P在y轴(不含原点)上运动,过点P作线段PM交x轴于点M,使| MP |
| PF |
| MP |
| PN |
(Ⅰ)求动点N的轨迹C的方程;
(Ⅱ)直线L与轨迹C交于A、B两点,如果
| OA |
| OB |
| AB |
| 6 |
分析:(Ⅰ)直接利用条件求方程.
(2)分斜率不存在和斜率存在两种情况求直线方程,运用弦长公式.
(2)分斜率不存在和斜率存在两种情况求直线方程,运用弦长公式.
解答:解:(Ⅰ)设N(x,y),P(0,p),
由题意知,P为MN的中点,∴M(-x,2p-y),
又M在x轴上,∴2p-y=0,即p=
,∴P(0,
),M(-x,0)
∵
•
=0,∴(-x,-
)×(1,-
)=0,∴y2=4x(x>0)
∴动点N的轨迹C的方程为y2=4x(x>0)
(Ⅱ)若直线L的斜率不存在,设直线L的方程为x=a>0,
此时,A(a,2
),B(a,-2
),
•
=a2-4a=-4,
∴a=2,
=(0,-4
),|AB|=4
¹4
,不符合题意,舍去.
∴直线L的斜率存在.
设直线L的方程为y=kx+b,A(
,y1)、B(
,y2),
由
消去y整理得,ky2-4y+4b=0,
△=16-16kb>0,y1+y2=
,
y1y2=
•
=
+y1y2=
=-4,
∴b=-2k,∴y1y2=-8
|AB|=
=
=
,
∵|AB|=4
∴
=4
4k4-3k2-1=0
∴k=±1∴当k=1时,b=-2,
当k=-1时,b=2;
所以直线L的方程为 y=x-2或y=-x+2.
由题意知,P为MN的中点,∴M(-x,2p-y),
又M在x轴上,∴2p-y=0,即p=
| y |
| 2 |
| y |
| 2 |
∵
| PM |
| PF |
| y |
| 2 |
| y |
| 2 |
∴动点N的轨迹C的方程为y2=4x(x>0)
(Ⅱ)若直线L的斜率不存在,设直线L的方程为x=a>0,
此时,A(a,2
| a |
| a |
| OA |
| OB |
∴a=2,
| AB |
| 2 |
| 2 |
| 6 |
∴直线L的斜率存在.
设直线L的方程为y=kx+b,A(
| ||
| 4 |
| ||
| 4 |
由
|
△=16-16kb>0,y1+y2=
| 4 |
| k |
y1y2=
| 4b |
| k |
| OA |
| OB |
| ||||
| 16 |
| b2+4kb |
| k2 |
∴b=-2k,∴y1y2=-8
|AB|=
(1+
|
|
| 4 |
| k2 |
| (k2+1)(1+2k2) |
∵|AB|=4
| 6 |
| 4 |
| k2 |
| (k2+1)(1+2k2) |
| 6 |
4k4-3k2-1=0
∴k=±1∴当k=1时,b=-2,
当k=-1时,b=2;
所以直线L的方程为 y=x-2或y=-x+2.
点评:注意分类讨论的解题思想,运用弦长公式.

练习册系列答案
相关题目
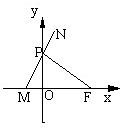 如图,已知定点F(1,0),动点P在y轴上运动,过点P作PM⊥PF并交x轴于M点,延长MP到N,使|PN|=|PM|.
如图,已知定点F(1,0),动点P在y轴上运动,过点P作PM⊥PF并交x轴于M点,延长MP到N,使|PN|=|PM|. (2011•潍坊二模)如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是4
(2011•潍坊二模)如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是4