题目内容
已知直线l与函数f(x)=lnx的图象相切于点(1,0),且l与函数 (m<0)的图象也相切.
(m<0)的图象也相切.(Ⅰ)求直线l的方程及m的值;
(Ⅱ)设
 ,若
,若 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【答案】分析:(Ⅰ)求出f′(x)得到斜率k=f′(1),且过(1,0),写出直线方程即可.因为直线l与g(x)的图象相切联立两个函数解析式,消去y得到一元二次方程,根的判别式=0即可求出m;
(Ⅱ)把g(x)代入到h(x)得a大于一个函数,求出导函数=0时x的值,再根据自变量的取值范围讨论函数的增减性得到函数的最大值,让a大于最大值即可求出a的范围.
解答:解:(Ⅰ)∵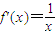 ,直线l是函数f(x)=lnx的图象在点(1,0)处的切线,
,直线l是函数f(x)=lnx的图象在点(1,0)处的切线,
∴其斜率为k=f′(1)=1
∴直线l的方程为y=x-1.
又因为直线l与g(x)的图象相切,
由 ,
,
得△=(m-1)2-9=0⇒m=-2(m=4不合题意,舍去)
(Ⅱ)∵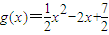
由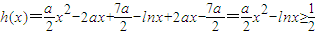 恒成立,
恒成立,
得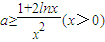 恒成立
恒成立
设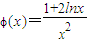 ,则
,则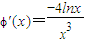
当0<x<1时,ϕ′(x)>0;当x>1时,ϕ′(x)<0.
于是,ϕ(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
故φ(x)的最大值为ϕmax(x)=ϕ(1)=1
要使a≥ϕ(x)恒成立,只需a≥1,
∴a的取值范围为[1,+∞)
点评:考查学生理解函数恒成立时取条件的能力,明白导数的几何意义,利用导数求曲线上某点切线方程的能力.
(Ⅱ)把g(x)代入到h(x)得a大于一个函数,求出导函数=0时x的值,再根据自变量的取值范围讨论函数的增减性得到函数的最大值,让a大于最大值即可求出a的范围.
解答:解:(Ⅰ)∵
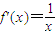 ,直线l是函数f(x)=lnx的图象在点(1,0)处的切线,
,直线l是函数f(x)=lnx的图象在点(1,0)处的切线,∴其斜率为k=f′(1)=1
∴直线l的方程为y=x-1.
又因为直线l与g(x)的图象相切,
由
 ,
,得△=(m-1)2-9=0⇒m=-2(m=4不合题意,舍去)
(Ⅱ)∵
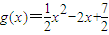
由
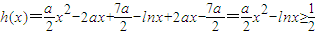 恒成立,
恒成立,得
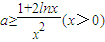 恒成立
恒成立设
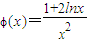 ,则
,则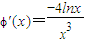
当0<x<1时,ϕ′(x)>0;当x>1时,ϕ′(x)<0.
于是,ϕ(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
故φ(x)的最大值为ϕmax(x)=ϕ(1)=1
要使a≥ϕ(x)恒成立,只需a≥1,
∴a的取值范围为[1,+∞)
点评:考查学生理解函数恒成立时取条件的能力,明白导数的几何意义,利用导数求曲线上某点切线方程的能力.

练习册系列答案
相关题目
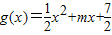 (m<0)的图象也相切.
(m<0)的图象也相切.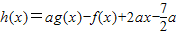 ,若
,若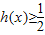 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.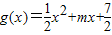 (m<0)的图象也相切.
(m<0)的图象也相切.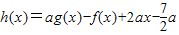 ,若
,若 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.