题目内容

中心在原点，焦点在x轴上的双曲线的实轴与虚轴相等，一个焦点到一条渐近线的距离为
2
，则双曲线方程为
 
．
分析：先根据双曲线的实轴与虚轴相等 设双曲线方程，求得焦点坐标和渐近线，进而根据点到直线的距离求得焦点到一条渐近线的距离的表达式求得a，进而求得双曲线方程．
解答：解：∵双曲线的实轴与虚轴相等
∴a=b
设双曲线
x2
a2
-
y2
a2
=1
一个焦点为（
2
a，0），渐近线为y=x
由点到直线距离公式可得
|
2
a|
2
=
2

∴a=
2

所以双曲线方程为
x2
2
-
y2
2
=1，即x2-y2=2
故答案为x2-y2=2
点评：本题主要考查了双曲线的标准方程．解题的关键是熟练掌握双曲线标准方程中a，b和c的关系．
练习册系列答案
相关题目
已知椭圆w的中心在原点，焦点在x轴上，长轴长为4，离心率为
6
3
，△ABC的顶点A，B在椭圆w上，C在直线l：y=x+2上，且AB∥l．
（1）求椭圆w的方程；
（2）当AB边通过坐标原点O时，求AB的长及△ABC的面积；
（3）当∠ABC=90°，且斜边AC的长最大时，求AB所在直线的方程．
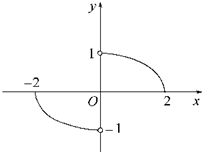精英家教网如图，函数y=f（x）的图象是中心在原点、焦点在x轴上的椭圆的两段弧，则不等式f（x）＜f（-x）+x的解集为（　　）
A、{x|-
2
＜x＜0或
2
＜x≤2}
B、{x|-2≤x＜-
2
或
2
＜x≤2}
C、{x|-2≤x＜-
2
2
或
2
2
＜x≤2}
D、{x|-
2
＜x＜
2
，且x≠0}
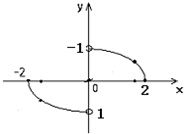精英家教网如图，函数y=f（x）的图象是中心在原点，焦点在x轴上的椭圆的两段弧，则不等式f（x）＜f（-x）+x的解集为（　　）
A、{
2
2
＜x≤2或
2
2
＜x≤2}
B、{x|-2≤x＜
2
或
2
＜x≤2}
C、{x|-
2
＜x＜0或
2
＜x≤2}
D、{x|-
2
＜x＜
2
，且x≠0}

（12分）

    已知椭圆中心在原点，焦点在x轴上，长轴长等于12，离心率为.

（Ⅰ）求椭圆的标准方程；

（Ⅱ）过椭圆左顶点作直线l垂直于x轴，若动点M到椭圆右焦点的距离比它到直线l的距离小4，求点M的轨迹方程.

 
已知椭圆w的中心在原点，焦点在x轴上，长轴长为4，离心率为
6
3
，△ABC的顶点A，B在椭圆w上，C在直线l：y=x+2上，且AB∥l．
（1）求椭圆w的方程；
（2）当AB边通过坐标原点O时，求AB的长及△ABC的面积；
（3）当∠ABC=90°，且斜边AC的长最大时，求AB所在直线的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网