题目内容
已知{an}为等差数列,Sn为其前n项和,若a1= ,S2=a3,则a2=________,Sn=________.
,S2=a3,则a2=________,Sn=________.
1 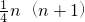
分析:根据等差数列的性质可求出公差,从而可求出第二项,以及等差数列的前n项和.
解答:根据{an}为等差数列,S2=a1+a2=a3= +a2;
+a2;
∴d=a3-a2=
∴a2= +
+ =1
=1
Sn=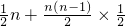 =
=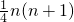
故答案为:1,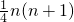
点评:本题主要考查了等差数列的前n项和,以及等差数列的通项公式,属于容易题.
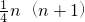
分析:根据等差数列的性质可求出公差,从而可求出第二项,以及等差数列的前n项和.
解答:根据{an}为等差数列,S2=a1+a2=a3=
 +a2;
+a2;∴d=a3-a2=

∴a2=
 +
+ =1
=1Sn=
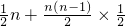 =
=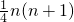
故答案为:1,
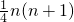
点评:本题主要考查了等差数列的前n项和,以及等差数列的通项公式,属于容易题.

练习册系列答案
相关题目