题目内容
设点P（x，y）是函数y=tanx与x+y=0图象的交点，则
的值是 ．
【答案】分析：由点P（x，y）是函数y=tanx与y=-x（x＞0）的图象的一个交点，可得出x2=tan2x，代入（x2+1）（cos2x+1）化简求值即可得到所求答案．
解答：解：：∵点P（x，y）是函数y=tanx与y=-x（x＞0）的图象的一个交点，∴x2=tan2x．
∴（x2+1）（cos2x+1）=（tan2x+1）（cos2x+1）=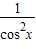
×2cos2x=2，
故答案为 2．
点评：本题考查正切函数的图象，解题的关键是根据P（x，y）是函数y=tanx与y=-x（x＞0）的图象的一个交点得出x2=tan2x，从而把求值的问题转化到三角函数中，得以顺利解题．
解答：解：：∵点P（x，y）是函数y=tanx与y=-x（x＞0）的图象的一个交点，∴x2=tan2x．
∴（x2+1）（cos2x+1）=（tan2x+1）（cos2x+1）=
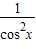×2cos2x=2，故答案为 2．
点评：本题考查正切函数的图象，解题的关键是根据P（x，y）是函数y=tanx与y=-x（x＞0）的图象的一个交点得出x2=tan2x，从而把求值的问题转化到三角函数中，得以顺利解题．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
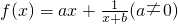的图象过点（0，-1）且与直线y=-1有且只有一个公共点；设点P（x0，y0）是函数y=f（x）图象上任意一点，过点P分别作直线y=x和直线x=1的垂线，垂足分别是M，N．