题目内容
6.已知a∈R,函数f(x)=x|x-a|,(1)当a=4时,写出函数y=f(x)的单调递增区间;
(2)当a=4时,求f(x)在区间(1,$\frac{9}{2}$)上最值;
(3)设a≠0,函数f(x)在(m,n)上既有最大值又有最小值,请分别求出m、n的取值范围(用a表示).
分析 (1)将a=4代入函数的解析得出f(x)=x|x-4|,将其变为分段函数,利用二次函数的图象与性质研究其单调性即可
(2)当a=4时,根据函数的图象和单调性,进行求解即可求最值.
(3)a≠0,函数f(x)在(m,n)上既有最大值又有最小值说明在函数最值不在区间端点处取得,在这个区间内必有两个极值,由函数的性质确定出极值,由于极值即为最值,故可借助函数的图象得m、n的取值范围.
解答 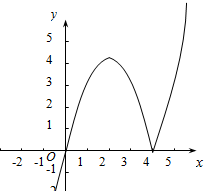 解:(1)当a=4时,f(x)=x|x-4|=$\left\{\begin{array}{l}{x(z-4),}&{x≥4}\\{x(4-x),}&{x<4}\end{array}\right.$,对应的图象为:
解:(1)当a=4时,f(x)=x|x-4|=$\left\{\begin{array}{l}{x(z-4),}&{x≥4}\\{x(4-x),}&{x<4}\end{array}\right.$,对应的图象为:
由二次函数的性质知,单调递增区间为(-∞,2],[4,+∞)(开区间不扣分)
(2)因为a>2,x∈[1,2]时,所以f(x)=x(a-x)=-x2+ax=$-{(x-\frac{a}{2})^2}+\frac{a^2}{4}$
当1<$\frac{a}{2}$≤$\frac{3}{2}$,即2<a≤3时,f(x)min=f(2)=2a-4
当$\frac{a}{2}$$>\frac{3}{2}$,即a>3时,f(x)min=f(1)=a-1
∴$f{(x)_{min}}=\left\{\begin{array}{l}2a-4,2<a≤3\\ a-1,a>3\end{array}\right.$
当a=4时,函数f(x)在区间(1,2]上递增,则[2,4]上递减,则[4,$\frac{9}{2}$)上递增,
∵f(2)=4,f(4)=0,
∴此时函数的最大值为4,最小值为0.
(Ⅲ)$f(x)=\left\{\begin{array}{l}x(x-a),x≥a\\ x(a-x),x<a\end{array}\right.$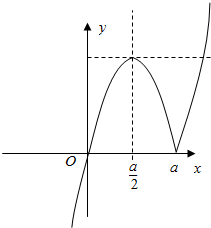

①当a>0时,图象如上图左所示
由$\left\{\begin{array}{l}y=\frac{a^2}{4}\\ y=x(x-a)\end{array}\right.$得$x=\frac{{(\sqrt{2}+1)a}}{2}$
∴$0≤m<\frac{a}{2}$,$a<n≤\frac{{\sqrt{2}+1}}{2}a$
②当a<0时,图象如上图右所示
由$\left\{\begin{array}{l}y=-\frac{a^2}{4}\\ y=x(a-x)\end{array}\right.$得$x=\frac{{(1+\sqrt{2)}}}{2}a$
∴$\frac{{1+\sqrt{2}}}{2}a≤m<a$,$\frac{a}{2}<n≤0$
点评 本题考点是函数的最值及其几何意义,综合考查了二次函数的图象,最值等知识以及配方法求最值的技巧.解题时数形结合,转化灵活,综合性很强.

| A. | 2 | B. | 0 | C. | 1 | D. | -1 |
| A. | $\sqrt{17}$ | B. | $\sqrt{61}$ | C. | $\sqrt{41}$ | D. | $\sqrt{37}$ |
| A. | y<x<1 | B. | x<y<1 | C. | 1<y<x | D. | 1<x<y |