题目内容
9.(理科)(1)已知f(x)=$\frac{1}{2}$sinx+sinx,求f′(x).(2)计算${∫}_{-π}^{0}$(cosx+ex)dx.
分析 (1)把f(x)合并同类项后利用基本初等函数的导数公式运算;
(2)求出被积函数的原函数,然后分别代入积分上限和积分下限后作差得答案.
解答 解:(1)∵f(x)=$\frac{1}{2}$sinx+sinx=$\frac{3}{2}sinx$,
∴f′(x)=$\frac{3}{2}cosx$;
(2)${∫}_{-π}^{0}$(cosx+ex)dx=$(sinx+{e}^{x}){|}_{-π}^{0}$=sin0+e0-sin(-π)-e-π=$1-\frac{1}{{e}^{π}}$.
点评 本题考查基本初等函数的导数公式,考查了定积分的求法,关键是求出被积函数的原函数,是基础题.

练习册系列答案
相关题目
14.下列区间中,能使函数y=sinx与函数y=cosx同时单调递减的是( )
| A. | [0,$\frac{π}{3}$] | B. | [$\frac{2π}{3}$,$\frac{3π}{4}$] | C. | [$\frac{7π}{6}$,$\frac{3π}{2}$] | D. | [$\frac{5π}{3}$,2π] |
1.如果圆(x+3)2+(y-1)2=1关于直线l:mx+4y-1=0对称,则直线l的斜率为( )
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
18.已知cos($\frac{π}{3}$+α)=-$\frac{1}{3}$,则sin(α-$\frac{π}{6}$)的值为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | -$\frac{2\sqrt{3}}{3}$ |
19.a、b表示两条直线,α、β、γ表示三个平面,下列命题中错误的是( )
| A. | a?α,b?α,且a∥β,b∥β,则α∥β | |
| B. | a、b是异面直线,则存在唯一的平面与a、b等距 | |
| C. | a⊥α,b?β,a⊥b,则α∥β | |
| D. | α⊥γ,γ∥β,a⊥α,b⊥β,则a⊥b |
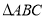 中,
中, ,则
,则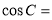 ( )
( )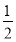 B.
B.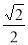 C.
C. D.
D.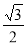
 如图l是东西走向的一水管,在水管北侧有两个半径都是10m的圆形蓄水池A,B(A,B分别为蓄水池的圆心),经测量,点A,B到水管l的距离分别为55m和25m,AB=50m.以l所在直线为x轴,过点A且与l垂直的直线为y轴,建立如图所示的直角坐标系(O为坐标原点).
如图l是东西走向的一水管,在水管北侧有两个半径都是10m的圆形蓄水池A,B(A,B分别为蓄水池的圆心),经测量,点A,B到水管l的距离分别为55m和25m,AB=50m.以l所在直线为x轴,过点A且与l垂直的直线为y轴,建立如图所示的直角坐标系(O为坐标原点).