题目内容
 已知函数f(x)=
已知函数f(x)=
|
(Ⅰ)求f(f(-3))及f(1-log0.253)的值;
(Ⅱ)当-5≤x<3时,在坐标系中作出函数f(x)的图象并求值域.
分析:(Ⅰ)利用分段函数分别代入进行求值即可.
(Ⅱ)根据分段函数的表达式求值域即可.
(Ⅱ)根据分段函数的表达式求值域即可.
解答:解:(Ⅰ)由分段函数可知f(f(-3))=f(2)及=5-22=5-4=1,
f(1-log0.253)=f(1+
log23)=f(log 22
)=5-2
;
(Ⅱ)函数图象为:
①当-5≤x<0,f(x)=-x-1∈(-1,4],
②当x=0时,f(0)=2,
③当0<x<3时,f(x)=5-2x∈(-3,4),
综上f(x)的值域为(-3,4].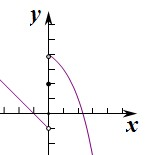
f(1-log0.253)=f(1+
| 1 |
| 2 |
| 3 |
| 3 |
(Ⅱ)函数图象为:
①当-5≤x<0,f(x)=-x-1∈(-1,4],
②当x=0时,f(0)=2,
③当0<x<3时,f(x)=5-2x∈(-3,4),
综上f(x)的值域为(-3,4].
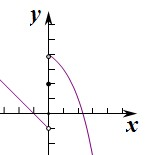
点评:本题主要考查分段函数的应用,注意分段函数的取值范围,比较基础.

练习册系列答案
相关题目