题目内容
△ABC中,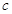 =
=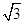 ,
,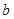 =1,B=30°,则△ABC的面积等于( )
=1,B=30°,则△ABC的面积等于( )
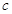 =
=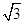 ,
,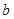 =1,B=30°,则△ABC的面积等于( )
=1,B=30°,则△ABC的面积等于( )A.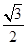 | B.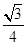 |
C.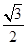 或 或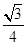 | D.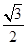 或 或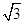 |
C
解:由已知,结合正弦定理可得b:sinB ="c" :sinC
,从而可求sinC及C,利用三角形的内角和公式计算A,利用三角形的面积公式S△ABC =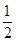 bcsinA进行计算可求,选C
bcsinA进行计算可求,选C
解:△ABC中,c="AB=" 3 ,b=AC=1.B=30°
由正弦定理可得 3 : sinC ="1:" sin300,sinC=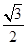
b<c∴C>B=30°
∴C=60°,或C=120°
当C=60°时,A=90°,S△ACB=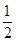 bcsinA="1" 2 ×1× 3 ×1= 3 2
bcsinA="1" 2 ×1× 3 ×1= 3 2
当C=120°时,A=30°,S△ABC=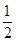 ×1×
×1× 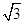 ×
× 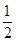 =
= 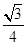
故答案为:C
,从而可求sinC及C,利用三角形的内角和公式计算A,利用三角形的面积公式S△ABC =
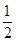 bcsinA进行计算可求,选C
bcsinA进行计算可求,选C解:△ABC中,c="AB=" 3 ,b=AC=1.B=30°
由正弦定理可得 3 : sinC ="1:" sin300,sinC=
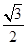
b<c∴C>B=30°
∴C=60°,或C=120°
当C=60°时,A=90°,S△ACB=
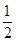 bcsinA="1" 2 ×1× 3 ×1= 3 2
bcsinA="1" 2 ×1× 3 ×1= 3 2 当C=120°时,A=30°,S△ABC=
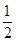 ×1×
×1× 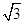 ×
× 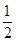 =
= 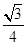
故答案为:C

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
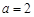 ,
, ,
, .
. .
.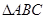 中,内角
中,内角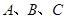 的对边分别是
的对边分别是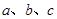 ,已知
,已知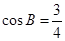
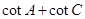 的值 (Ⅱ)设
的值 (Ⅱ)设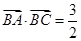 ,求
,求 的值。
的值。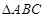 中,内角A、B、C依次成等差数列,
中,内角A、B、C依次成等差数列,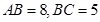 ,则
,则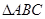 中,若
中,若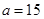 ,
,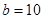 ,
,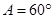 ,则
,则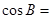 ( )
( )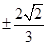
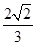
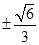
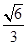
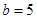 ,
,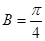 ,
,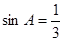 ,则
,则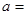

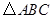 中,
中,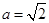 ,
,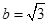 ,
,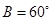 ,那么角
,那么角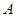 等于
等于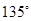
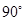
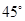
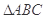 中,
中,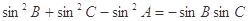 ,则A= ( )
,则A= ( )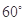
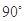


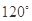
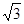 ,AC=2,则△ABC的面积是______。
,AC=2,则△ABC的面积是______。