题目内容
已知数列an中,a1=| 1 | 2 |
分析:(1)将点代入直线的方程,得到{an}相邻项的关系,求出
为常数,利用等比数列的定义证得结论.
(2)利用等比数列的通项公式求出bn,利用逐差相加法求出an,利用分组法求出数列的前n项和.
| bn+1 |
| bn |
(2)利用等比数列的通项公式求出bn,利用逐差相加法求出an,利用分组法求出数列的前n项和.
解答:解:(1)由已知得a1=
,2an+1=an+n
∴a2=
则a2-a1-1=-
∴
=
=
∴数列{bn}是以-
为首项,以
为公比的等比数列
(2)由(1)知,bn=-
×(
)n-1=-
×
∴an+1-an-1=-
×
得an-an-1=-
×
+1
…
a3-a2=-
×
+1
a2-a1=-
×
+1
各式相乘得an-a1=-
(
+
+…+
)+(n-1)
∴an=a1+n-1-
×
=
+n-2
∵Sn=3(
+
+…+
)+(1+2+3+…+n)-2n=-
+
+3
| 1 |
| 2 |
∴a2=
| 3 |
| 4 |
| 3 |
| 4 |
∴
| bn+1 |
| bn |
| an+2-an+1-1 |
| an+1-an-1 |
| 1 |
| 2 |
∴数列{bn}是以-
| 3 |
| 4 |
| 1 |
| 2 |
(2)由(1)知,bn=-
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2n |
∴an+1-an-1=-
| 3 |
| 2 |
| 1 |
| 2n |
得an-an-1=-
| 3 |
| 2 |
| 1 |
| 2n-1 |
…
a3-a2=-
| 3 |
| 2 |
| 1 |
| 22 |
a2-a1=-
| 3 |
| 2 |
| 1 |
| 2 |
各式相乘得an-a1=-
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
∴an=a1+n-1-
| 3 |
| 2 |
| ||||
1-
|
=
| 3 |
| 2n |
∵Sn=3(
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
| 3 |
| 2n |
| n2-3n |
| 2 |
点评:求数列的前n项和关键判断出通项的特点,再选择合适的方法求和.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
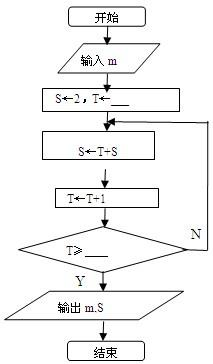 16、已知数列an中,a1=2,且an=n+an-1(n≥2),求这个数列的第m项am的值(m≥2).现给出此算法流程图的一部分如图.
16、已知数列an中,a1=2,且an=n+an-1(n≥2),求这个数列的第m项am的值(m≥2).现给出此算法流程图的一部分如图.