题目内容
已知数列an中,a1=1,a2=a-1(a≠1,a为实常数),前n项和Sn恒为正值,且当n≥2时,| 1 |
| Sn |
| 1 |
| an |
| 1 |
| an+1 |
(1)求证:数列Sn是等比数列;
(2)设an与an+2的等差中项为A,比较A与an+1的大小;
(3)设m是给定的正整数,a=2.现按如下方法构造项数为2m有穷数列bn:当k=m+1,m+2,…,2m时,bk=ak•ak+1;当k=1,2,…,m时,bk=b2m-k+1.求数列{bn}的前n项和为Tn(n≤2m,n∈N*).
分析:(1)直接利用an和Sn的关系:an=Sn-Sn-1 (n≥2)代入
=
-
整理可得Sn2=Sn-1Sn+1再检验前两项是否成立即可证明结论.
(2)先由(1)的结论结合an和Sn的关系:an=Sn-Sn-1 (n≥2)求出数列的通项;在让A与an+1作差,利用Sn恒为正值对a进行讨论即可比较大小;
(3)由条件可得当m+1≤k≤2m时,bk=ak•ak+1=22k-3.然后分n≤m以及m+1≤n≤2m两种情况转化后直接代入等比数列的求和公式即可.
| 1 |
| Sn |
| 1 |
| an |
| 1 |
| an+1 |
(2)先由(1)的结论结合an和Sn的关系:an=Sn-Sn-1 (n≥2)求出数列的通项;在让A与an+1作差,利用Sn恒为正值对a进行讨论即可比较大小;
(3)由条件可得当m+1≤k≤2m时,bk=ak•ak+1=22k-3.然后分n≤m以及m+1≤n≤2m两种情况转化后直接代入等比数列的求和公式即可.
解答:解:(1)当n≥3时,
=
-
=
-
,
化简得Sn2=Sn-1Sn+1(n≥3),又由a1=1,a2=a-1得
=
-
,
解得a3=a(a-1),∴S1=1,S2=a,S3=a2,也满足Sn2=Sn-1Sn+1,而Sn恒为正值,
∴数列{Sn}是等比数列.(4分)
(2)Sn的首项为1,公比为a,Sn=an-1.
当n≥2时,an=Sn-Sn-1=(a-1)an-2,
∴an=
当n=1时,A-an+1=
-a2=
=
[(a-
)2+
]≥
,此时A>an+1.(6分)
当n≥2时,A-an+1=
-an+1=
-(a-1)an-1=
=
.
∵Sn恒为正值∴a>0且a≠1,
若0<a<1,则A-an+1<0,若a>1,则A-an+1>0.
综上可得,当n=1时,A>an+1;
当n≥2时,若0<a<1,则A<an+1,
若a>1,则A>an+1.(10分)
(3)∵a=2∴an=
,当m+1≤k≤2m时,bk=ak•ak+1=22k-3.
若n≤m,n∈N*,则由题设得b1=b2m,b2=b2m-1,bn=b2m-n+1
Tn=b1+b2+…+bn=b2m-1+…+b2m-n+1
=24m-3+24m-5+…+24m-2n-1=
=
.(13分)
若m+1≤n≤2m,n∈N*,则Tn=bm+bm+1+bm+2+…+bn=
+22m-1+22m+1+…+22n-3
=
+
=
.
综上得Tn=
.(16分)
| 1 |
| Sn |
| 1 |
| an |
| 1 |
| an+1 |
| 1 |
| Sn-Sn-1 |
| 1 |
| Sn+1-SN |
化简得Sn2=Sn-1Sn+1(n≥3),又由a1=1,a2=a-1得
| 1 |
| a |
| 1 |
| a-1 |
| 1 |
| a3 |
解得a3=a(a-1),∴S1=1,S2=a,S3=a2,也满足Sn2=Sn-1Sn+1,而Sn恒为正值,
∴数列{Sn}是等比数列.(4分)
(2)Sn的首项为1,公比为a,Sn=an-1.
当n≥2时,an=Sn-Sn-1=(a-1)an-2,
∴an=
|
当n=1时,A-an+1=
| a1+a3 |
| 2 |
| a2-3a+3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
当n≥2时,A-an+1=
| an+an+2 |
| 2 |
| (a-1)an-2+(a-1)an |
| 2 |
| (a-1)an-2(a2-2a+1) |
| 2 |
| (a-1)3an-2 |
| 2 |
∵Sn恒为正值∴a>0且a≠1,
若0<a<1,则A-an+1<0,若a>1,则A-an+1>0.
综上可得,当n=1时,A>an+1;
当n≥2时,若0<a<1,则A<an+1,
若a>1,则A>an+1.(10分)
(3)∵a=2∴an=
|
若n≤m,n∈N*,则由题设得b1=b2m,b2=b2m-1,bn=b2m-n+1
Tn=b1+b2+…+bn=b2m-1+…+b2m-n+1
=24m-3+24m-5+…+24m-2n-1=
| 24m-3(1-4-n) |
| 1-4-1 |
| 24m-1(1-2-2n) |
| 3 |
若m+1≤n≤2m,n∈N*,则Tn=bm+bm+1+bm+2+…+bn=
| 24m-1(1-2-2m) |
| 3 |
=
| 24m-1(1-2-2m) |
| 3 |
| 22m-1(1-4n-m) |
| 1-4 |
| 24m-1+22n-1 |
| 3 |
综上得Tn=
|
点评:本题第二问考查了已知前n项和为Sn求数列{an}的通项公式,根据an和Sn的关系:an=Sn-Sn-1 (n≥2)求解数列的通项公式.另外,须注意公式成立的前提是n≥2,所以要验证n=1时通项是否成立,若成立则:an=Sn-Sn-1 (n≥1);若不成立,则通项公式为分段函数.

练习册系列答案
相关题目
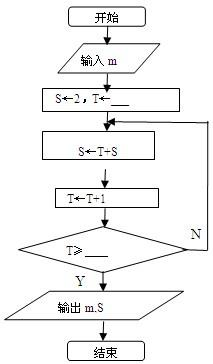 16、已知数列an中,a1=2,且an=n+an-1(n≥2),求这个数列的第m项am的值(m≥2).现给出此算法流程图的一部分如图.
16、已知数列an中,a1=2,且an=n+an-1(n≥2),求这个数列的第m项am的值(m≥2).现给出此算法流程图的一部分如图.