题目内容
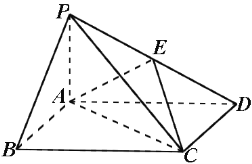
【题目】【2014高考课标2理数18】如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，
E为PD的中点.
（Ⅰ）证明：PB∥平面AEC；
（Ⅱ）设二面角D-AE-C为60°，AP=1，AD=
，求三棱锥E-ACD的体积.
【答案】
【解析】（Ⅰ）证明：设O为AC与BD交点，连结OE，则由矩形ABCD知：O为BD的中点，因为E是BD的中点，所以OE∥PB，因为OE
面AEC，PB
面AEC，所以PB∥平面AEC。
（Ⅱ）以A为原点，直线AB、AD、AP分别为x、y、z轴建立空间直角坐标系，设AB=m，则
是平面AED的一个法向量，设
是平面AEC的法向量，则
，解得
，
，所以令
，得
，所以
=
，因为二面角的大小与其两个半平面的两个法向量的夹角相等哉互补，所以=
，解得
，因为E是PD的中点，所以三棱锥E-ACD的高为
，所以三棱锥E-ACD的体积为
=
=
.
练习册系列答案
口算题天天练系列答案
相关题目
