Question

已知函数f（x）=ax²-|x|+2a-1（a为实常数）．
（1）若a=1，作函数f（x）的图象；
（2）设f（x）在区间[1，2]上的最小值为g（a），求g（a）的表达式．

Answer 1

分析：（1）对于含有绝对值的函数图象，用分类讨论的方法；
（2）对于二次函数在某个区间上的最值问题，考虑其对称轴与区间的相对位置，进行讨论．

解答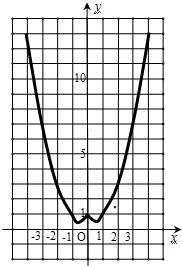：解：（1）当a=1时，f（x）=x²-|x|+1=

x2+x+1，x＜0 x2-x+1，x≥0

．作图（如图所示）
（2）当x∈[1，2]时，f（x）=ax²-x+2a-1．
若a=0，则f（x）=-x-1在区间[1，2]上是减函数，g（a）=f（2）=-3．
若a≠0，则f(x)=a(x-

1

2a

)2+2a-

1

4a

-1，
f（x）图象的对称轴是直线x=

1

2a

．
当a＜0时，f（x）在区间[1，2]上是减函数，g（a）=f（2）=6a-3．
当0＜

1

2a

＜1，即a＞

1

2

时，
f（x）在区间[1，2]上是增函数，g（a）=f（1）=3a-2．
当1≤

1

2a

≤2，即

1

4

≤a≤

1

2

时，g（a）=f（

1

2a

）=2a-

1

4a

-1．
当

1

2a

＞2，即0＜a＜

1

4

时，f（x）在区间[1，2]上是减函数，g（a）=f（2）=6a-3．
综上可得，g(a)=

6a-3，a＜ 1 4 2a- 1 4a -1， 1 4 ≤a≤ 1 2 3a-2，a＞ 1 2

．

点评：含有参数的二次函数在某区间上的最值问题，通常有二种情形：1、动对称轴；2、对区间的．本题属于第一种情形，解决的办法是分类讨论．