Question

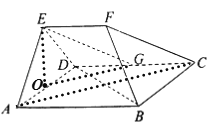
【题目】在以ABCDEF为顶点的五面体中，底面ABCD为菱形，∠ABC＝120°，AB＝AE＝ED＝2EF，EFAB，点G为CD中点，平面EAD⊥平面ABCD.

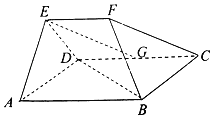
（1）证明：BD⊥EG；

（2）若三棱锥，求菱形ABCD的边长.

Answer 1

【答案】（1）详见解析；（2）.

【解析】

（1）取中点，连，可得，结合平面EAD⊥平面ABCD，可证

平面ABCD，进而有，再由底面是菱形可得，可得，

可证得平面，即可证明结论；

（2）设底面边长为，由EFAB，AB＝2EF，，求出体积，建立的方程，即可求出结论.

（1）取中点，连，

底面ABCD为菱形，，

，平面EAD⊥平面ABCD，

平面平面平面，

平面平面，

底面ABCD为菱形，，

为中点，，

平面，

平面平面，；

（2）设菱形ABCD的边长为，则，

，

，

，

，所以菱形ABCD的边长为.