题目内容
B(文)设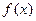 是定义在
是定义在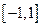 上的偶函数,当
上的偶函数,当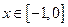 时,
时,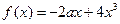 222233.
222233.
(1)若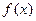 在
在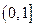 上为增函数,求
上为增函数,求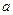 的取值范围;
的取值范围;
(2)是否存在正整数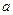 ,使
,使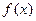 的图象的最高点落在直线
的图象的最高点落在直线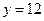 上?若存在,求出
上?若存在,求出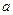 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
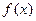 是定义在
是定义在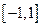 上的偶函数,当
上的偶函数,当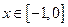 时,
时,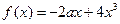 222233.
222233.(1)若
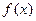 在
在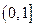 上为增函数,求
上为增函数,求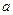 的取值范围;
的取值范围;(2)是否存在正整数
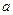 ,使
,使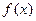 的图象的最高点落在直线
的图象的最高点落在直线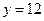 上?若存在,求出
上?若存在,求出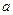 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(1)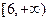 ;
;
(2)存在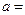 8满足题设
8满足题设
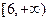 ;
;(2)存在
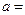 8满足题设
8满足题设因为当 ∈[-1,0]时,
∈[-1,0]时,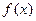
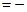 2a
2a +4
+4 3222233.
3222233.
所以当 ∈
∈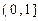 时,
时,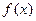 =
=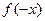 =2a
=2a -4
-4 3,
3,
∴ ………………………………………2分
………………………………………2分
(Ⅰ)由题设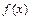 在
在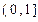 上为增函数,∴
上为增函数,∴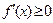 在
在 ∈
∈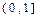 恒成立,
恒成立,
即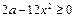 对
对 ∈
∈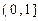 恒成立,于是,
恒成立,于是,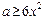 ,从而
,从而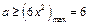 .
.
即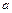 的取值范围是
的取值范围是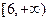 ………………………………6分
………………………………6分
(Ⅱ)因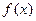 为偶函数,故只需研究函数
为偶函数,故只需研究函数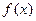 =2
=2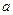
 -4
-4 3在
3在 ∈
∈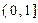 的最大值.
的最大值.
令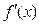 =2a-12
=2a-12 2=0,得
2=0,得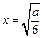 .……………8分
.……………8分
若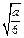 ∈
∈ ,即0<
,即0<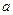 ≤6,则
≤6,则
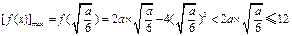 ,
,
故此时不存在符合题意的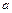 ;……………10分
;……………10分
若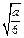 >1,即
>1,即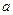 >6,则
>6,则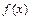 在
在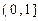 上为增函数,于是
上为增函数,于是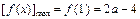 .
.
令2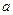 -4=12,故
-4=12,故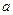 =8. 综上,存在
=8. 综上,存在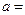 8满足题设.………………12分
8满足题设.………………12分
 ∈[-1,0]时,
∈[-1,0]时,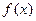
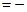 2a
2a +4
+4 3222233.
3222233.所以当
 ∈
∈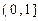 时,
时,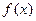 =
=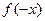 =2a
=2a -4
-4 3,
3,∴
 ………………………………………2分
………………………………………2分(Ⅰ)由题设
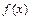 在
在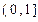 上为增函数,∴
上为增函数,∴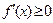 在
在 ∈
∈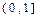 恒成立,
恒成立,即
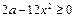 对
对 ∈
∈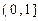 恒成立,于是,
恒成立,于是,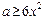 ,从而
,从而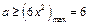 .
.即
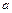 的取值范围是
的取值范围是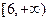 ………………………………6分
………………………………6分(Ⅱ)因
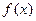 为偶函数,故只需研究函数
为偶函数,故只需研究函数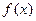 =2
=2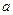
 -4
-4 3在
3在 ∈
∈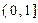 的最大值.
的最大值.令
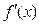 =2a-12
=2a-12 2=0,得
2=0,得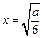 .……………8分
.……………8分若
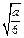 ∈
∈ ,即0<
,即0<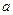 ≤6,则
≤6,则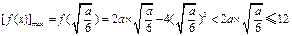 ,
,故此时不存在符合题意的
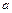 ;……………10分
;……………10分若
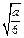 >1,即
>1,即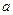 >6,则
>6,则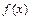 在
在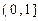 上为增函数,于是
上为增函数,于是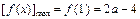 .
.令2
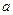 -4=12,故
-4=12,故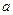 =8. 综上,存在
=8. 综上,存在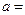 8满足题设.………………12分
8满足题设.………………12分 
练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
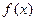 是定义在
是定义在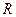 上的奇函数,且当
上的奇函数,且当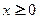 时,
时,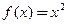 ,若对任意
,若对任意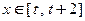 ,都有
,都有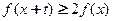 恒成立,则实数
恒成立,则实数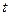 的取值范围是______________.
的取值范围是______________.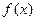 是
是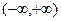 上的偶函数,若对于
上的偶函数,若对于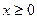 ,都有
,都有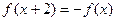 ,且当
,且当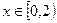 时,
时, 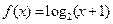 ,
,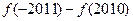 的值为 .
的值为 . 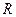 上的函数
上的函数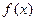 是奇函数,且
是奇函数,且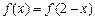 ,在区间[1,2]上是单调递减函数.关于函数
,在区间[1,2]上是单调递减函数.关于函数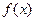 有下列结论:
有下列结论: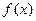 为定义在
为定义在 上的奇函数,当
上的奇函数,当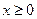 时,
时,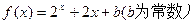 ,则
,则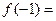 ( )
( ) 是定义在实数集
是定义在实数集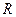 上的偶函数,且在
上的偶函数,且在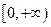 上是减函数,若
上是减函数,若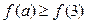 ,则实数
,则实数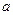 的取值范围是
的取值范围是 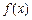 的定义域为
的定义域为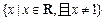 ,
,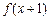 为偶函数,当
为偶函数,当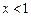 时,
时,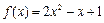 ,当
,当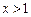 时,
时,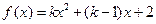 是偶函数,则
是偶函数,则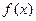 的递减区间是
的递减区间是
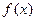 的定义域为R, 则“函数
的定义域为R, 则“函数 奇函数”的( )
奇函数”的( )