题目内容
已知两个命题r(x):sinx+cosx＞m,s(x):x2+mx+1＞0.如果对
x∈R,r(x)与s(x)有且仅有一个是真命题.求实数m的取值范围.
实数m的取值范围是m≤-2或-
≤m＜2
解析:
∵sinx+cosx=sin（x+
）≥-，
∴当r(x)是真命题时，m＜- 3分
又∵对
x∈R，s(x)为真命题，即x2+mx+1＞0恒成立，
有Δ=m2-4＜0,∴-2＜m＜2. 6分
∴当r(x)为真，s(x)为假时，m＜-，
同时m≤-2或m≥2,即m≤-2; 9分
当r(x)为假，s(x)为真时，m≥-且-2＜m＜2,
即-≤m＜2. 12分
综上，实数m的取值范围是m≤-2或-≤m＜2. 14分
练习册系列答案
相关题目
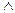s(x) 为假，r(x)
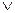s(x)为真，求实数m的取值范围。
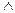s(x) 为假，r(x)
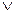s(x)为真，求实数m的取值范围。
s(x) 为假，r(x)
s(x)为真，求实数m的取值范围。
s(x) 为假，r(x)
s(x)为真，求实数m的取值范围。