题目内容
如果 是函数
是函数 图像上的点,
图像上的点, 是函数
是函数 图像上的点,且
图像上的点,且 两点之间的距离
两点之间的距离 能取到最小值
能取到最小值 ,那么将
,那么将 称为函数
称为函数 与
与 之间的距离.按这个定义,函数
之间的距离.按这个定义,函数 和
和 之间的距离是 .
之间的距离是 .
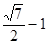
解析试题分析:作出函数y=f(x)图象与函数y=g(x)图象,如图
y=f(x)图象即抛物线y2=x的上半支,函数y=g(x)图象是以A(2,0)为圆心半径等于1的圆的上半圆。
问题转化成,找到点A与抛物线上一点的最近距离,再用这个距离减去圆的半径1,即为函数y=f(x)与y=g(x)之间的距离.
设动点B(t2,t)是y=f(x)图象上一点,则 ,所以,
,所以, 时,,|AB|的最小值为:
时,,|AB|的最小值为:
∴函数y=f(x)与y=g(x)之间的距离为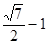 。
。
考点:本题主要考查幂函数的图象,二次函数的图象和性质。
点评:中档题,认识到y=f(x)图象是抛物线y2=x的上半支,函数y=g(x)图象是以A(2,0)为圆心半径等于1的圆的上半圆.只要找到点A与抛物线上一点的最近距离,再用这个距离减去圆的半径1,是解题的关键。

练习册系列答案
相关题目
 是偶函数;
是偶函数; 的值域为
的值域为 ;
; ,
, ,若
,若 ,则
,则 的取值集合为
的取值集合为 ;
; ,
, ,对应法则
,对应法则 ,则
,则 的映射;
的映射; ,若函数
,若函数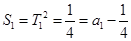 在区间
在区间 上是增函数,则
上是增函数,则 的取值范围是 .
的取值范围是 . ,则
,则 = .
= . 为奇函数,则
为奇函数,则
 等于 .
等于 . 的单调递增区间是________________.
的单调递增区间是________________. 在
在 处有极大值,则常数
处有极大值,则常数 的值为 ;
的值为 ; 的所有切线中,斜率最小的切线方程是 。
的所有切线中,斜率最小的切线方程是 。