题目内容
已知P在直线AB上,O不在直线AB上,且
=(2x-1)
+(x+2)
,则x=
| OP |
| OA |
| OB |
0
0
.分析:由已知中P在直线AB上,O不在直线AB上,且
=(2x-1)
+(x+2)
,根据三点共线的充要条件,我们可以构造出一个关于x的方程,解方程即可求出答案.
| OP |
| OA |
| OB |
解答:解:∵O不在直线AB上,P在直线AB上,
∴A、B、P共线
∴存在λ∈R,使
=λ
⇒
=(1-λ)
+λ
,
又∵
、
不共线,
⇒x=0.
故答案为:0
∴A、B、P共线
∴存在λ∈R,使
| AP |
| AB |
| OP |
| OA |
| OB |
又∵
| OA |
| OB |
|
故答案为:0
点评:本题考查的知识点是平行向量与共线向量,三点共线的充要条件(向量法),其中熟练掌握A、B、P共线?存在λ∈R,使
=λ
⇒
=(1-λ)
+λ
,是解答本题的关键.
| AP |
| AB |
| OP |
| OA |
| OB |

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
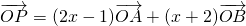 ,则x=________.
,则x=________.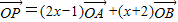 ,则x= .
,则x= .