题目内容
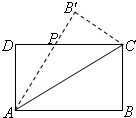 如图,设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后,交DC于P,设AB=x.
如图,设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后,交DC于P,设AB=x.(1)请用x来表示DP;
(2)请用x来表示△ADP的面积;
(3)请根据△ADP的面积表达式求此面积的最大值.
分析:(1)由AB=x可得AD=12-x,由DP=PB'可得AP=AB'-PB'=AB-DP=x-DP,
(2)利用勾股定理得 (12-x)2+DP2=(x-DP)2可求DP=12-
,从而可得△ADP的面积S=
AD•DP=
(12-x)•(12-
)=108-(6x+
),
(3)利用基本不等式可得6x+
≥2
=72
,从而可得S=108-(6x+
)≤108-72
.
(2)利用勾股定理得 (12-x)2+DP2=(x-DP)2可求DP=12-
| 72 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 72 |
| x |
| 432 |
| x |
(3)利用基本不等式可得6x+
| 432 |
| x |
6x•
|
| 2 |
| 432 |
| x |
| 2 |
解答: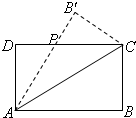 解:(1)∵AB=x,∴AD=12-x,
解:(1)∵AB=x,∴AD=12-x,
又DP=PB',AP=AB'-PB'=AB-DP=x-DP,
由勾股定理得 (12-x)2+DP2=(x-DP)2,得DP=12-
,
(2)结合(1)可得,△ADP的面积S=
AD•DP=
(12-x)•(12-
)
=108-(6x+
),
(3)∵x>0,∴6x+
≥2
=72
,
∴S=108-(6x+
)≤108-72
.
当且仅当6x=
时,即当x=6
时,S有最大值108-72
.
 解:(1)∵AB=x,∴AD=12-x,
解:(1)∵AB=x,∴AD=12-x,又DP=PB',AP=AB'-PB'=AB-DP=x-DP,
由勾股定理得 (12-x)2+DP2=(x-DP)2,得DP=12-
| 72 |
| x |
(2)结合(1)可得,△ADP的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 72 |
| x |
=108-(6x+
| 432 |
| x |
(3)∵x>0,∴6x+
| 432 |
| x |
6x•
|
| 2 |
∴S=108-(6x+
| 432 |
| x |
| 2 |
当且仅当6x=
| 432 |
| x |
| 2 |
| 2 |
点评:利用三角形知识解决实际问题,主要构造三角形或其它几何图形,借助于三角形的知识进行求解,而基本不等式的应用是求解函数最值的常用方法.

练习册系列答案
相关题目
 如图,设矩形ABCD(AB>AD)的周长为4,把它关于AC折起来,AB折过去后,交DC与点P.设AB=x,求△ADP的最大面积及相应的x的值.
如图,设矩形ABCD(AB>AD)的周长为4,把它关于AC折起来,AB折过去后,交DC与点P.设AB=x,求△ADP的最大面积及相应的x的值. 如图,设矩形ABCD(AB>AD)的周长为l(l为定值),把该矩形沿AC折起来,AB折过去后,交DC于点P,设AB=x,△ADP的面积为y.
如图,设矩形ABCD(AB>AD)的周长为l(l为定值),把该矩形沿AC折起来,AB折过去后,交DC于点P,设AB=x,△ADP的面积为y. 如图,设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后,交DC于P,设AB=x,
如图,设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后,交DC于P,设AB=x, (2011•黄冈模拟)如图,设矩形ABCD(AB>AD)的周长是20,把三角形ABC沿AC折起来,AB折过去后,交DC于点F,设AB=x,则三角形ADF的面积最大时的x的值为
(2011•黄冈模拟)如图,设矩形ABCD(AB>AD)的周长是20,把三角形ABC沿AC折起来,AB折过去后,交DC于点F,设AB=x,则三角形ADF的面积最大时的x的值为