题目内容
 如图,设矩形ABCD(AB>AD)的周长为4,把它关于AC折起来,AB折过去后,交DC与点P.设AB=x,求△ADP的最大面积及相应的x的值.
如图,设矩形ABCD(AB>AD)的周长为4,把它关于AC折起来,AB折过去后,交DC与点P.设AB=x,求△ADP的最大面积及相应的x的值.分析:由已知中矩形ABCD(AB>AD)的周长为4,AB=x,我们可以可得AD=2-x,进而设出PC=a,则DP=x-a,由勾股定理,我们可以得到△ADP的面积的表达式,进而由基本不等式我们易求出△ADP的最大面积及相应的x的值.
解答: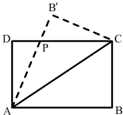 (本小题满分12分)
(本小题满分12分)
解:如图,因为AB=x,所以AD=2-x.…(2分)
设PC=a,则DP=x-a.
由勾股定理,得(2-x)2+(x-a)2=a2.…(4分)
可得a=
.DP=x-a=
.…(6分)
所以△ADP的面积S=
(2-x)
=
=-(x+
)+3.…(8分)
∵x>0,x+
≥2
=2
.…(10分)
∴S=-(x+
)+3≤3-2
.
当且仅当x=
时,即当x=
时取“=”号.
答:当x=
时,△ADP的最大面积为3-2
.…(12分)
 (本小题满分12分)
(本小题满分12分)解:如图,因为AB=x,所以AD=2-x.…(2分)
设PC=a,则DP=x-a.
由勾股定理,得(2-x)2+(x-a)2=a2.…(4分)
可得a=
| x2-2x+2 |
| x |
| 2x-2 |
| x |
所以△ADP的面积S=
| 1 |
| 2 |
| 2x-2 |
| x |
| -x2+3x-2 |
| x |
| 2 |
| x |
∵x>0,x+
| 2 |
| x |
x•
|
| 2 |
∴S=-(x+
| 2 |
| x |
| 2 |
当且仅当x=
| 2 |
| x |
| 2 |
答:当x=
| 2 |
| 2 |
点评:本题考查的知识点是函数模型的选择与应用,基本不等式的应用,其中根据已知条件求出△ADP的面积的表达式,将问题转化为利用基本不等式求最值问题,是解答本题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
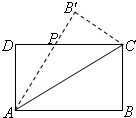 如图,设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后,交DC于P,设AB=x.
如图,设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后,交DC于P,设AB=x. 如图,设矩形ABCD(AB>AD)的周长为l(l为定值),把该矩形沿AC折起来,AB折过去后,交DC于点P,设AB=x,△ADP的面积为y.
如图,设矩形ABCD(AB>AD)的周长为l(l为定值),把该矩形沿AC折起来,AB折过去后,交DC于点P,设AB=x,△ADP的面积为y. 如图,设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后,交DC于P,设AB=x,
如图,设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后,交DC于P,设AB=x, (2011•黄冈模拟)如图,设矩形ABCD(AB>AD)的周长是20,把三角形ABC沿AC折起来,AB折过去后,交DC于点F,设AB=x,则三角形ADF的面积最大时的x的值为
(2011•黄冈模拟)如图,设矩形ABCD(AB>AD)的周长是20,把三角形ABC沿AC折起来,AB折过去后,交DC于点F,设AB=x,则三角形ADF的面积最大时的x的值为