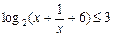题目内容
若不等式1-loga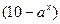
＜0有解，则实数a的范围是 .
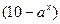＜0有解，则实数a的范围是 .（0，1）∪（1，10）
当a＞1时，不等式化为10-ax＞a,要使不等式有解，必须10-a＞0
∴1＜a＜10
当0＜a＜1时，不等式化为0＜10-ax＜a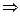
10-a＜ax＜10不等式恒有解
故满足条件a的范围是（0，1）∪（1，10）
∴1＜a＜10
当0＜a＜1时，不等式化为0＜10-ax＜a
10-a＜ax＜10不等式恒有解故满足条件a的范围是（0，1）∪（1，10）
练习册系列答案
相关题目
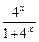，求证：f（1）+f（2）+…+f（n）>n+
.
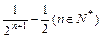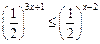； (2) log73x < log7(x2-4)．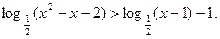
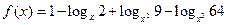，则使
的
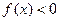的取值范围为（ ）
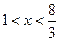
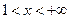
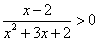的解集是( )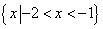
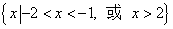
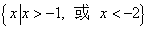
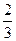＞1，则a的取值范围是 .