题目内容
已知f(x2-5)=loga
(a>0,且a≠1).
(1)求f(x)的解析式,并写出定义域;
(2)判断f(x)的奇偶性并证明;
(3)当a>1时,求使f(x)≥0成立的x的集合.
| x2 |
| 10-x2 |
(1)求f(x)的解析式,并写出定义域;
(2)判断f(x)的奇偶性并证明;
(3)当a>1时,求使f(x)≥0成立的x的集合.
:(1)令x2-5=t,则x2=t+5.
∴f(x2-5)=loga
化为f(t)═loga
=loga
.
∴f(x)=loga
,要使函数有意义,必须
>0,解得x∈(-5,5).
(2)∵函数的定义域关于原点对称,∴f(-x)=loga
=-loga
=-f(x).
∴函数是奇函数.
(3)当a>1时,f(x)≥0成立,
即loga
>0
⇒loga
>loga1,
∴
>1
⇒
-1>0
⇒
>0
⇒
<0,
解得x∈[0,5).
∴f(x2-5)=loga
| x2 |
| 10-x2 |
| t+5 |
| 10-t-5 |
| t+5 |
| 5-t |
∴f(x)=loga
| x+5 |
| 5-x |
| x+5 |
| 5-x |
(2)∵函数的定义域关于原点对称,∴f(-x)=loga
| -x+5 |
| 5-(-x) |
| x+5 |
| 5-x |
∴函数是奇函数.
(3)当a>1时,f(x)≥0成立,
即loga
| x+5 |
| 5-x |
⇒loga
| x+5 |
| 5-x |
∴
| x+5 |
| 5-x |
⇒
| x+5 |
| 5-x |
⇒
| x+5+x-5 |
| 5-x |
⇒
| 2x |
| x-5 |
解得x∈[0,5).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
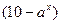 <0有解,则实数a的范围是 .
<0有解,则实数a的范围是 .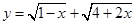 最大值.
最大值.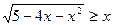 (2)
(2)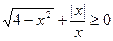
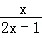 <0的解为 .
<0的解为 .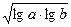 , Q=
, Q=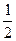 (lga+lgb),R="lg"
(lga+lgb),R="lg" 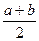 , 则 ( )
, 则 ( )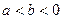 ,则下列不等式不能成立的是 ( )
,则下列不等式不能成立的是 ( )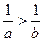
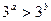
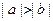
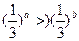
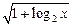 > 1 – log 2x的解是( )
> 1 – log 2x的解是( )