题目内容
已知函数f(x)=lnx-ax(a∈R).(1)求函数f(x)的极值点和极值;
(2)当a>0时,求函数f(x)在[1,2]上的最小值.
(3)当a=
 时,是否同时存在实数m和M(m<M),使得对每一个t∈[m,M],直线y=t与曲线y=f(x),x∈[1,2]都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
时,是否同时存在实数m和M(m<M),使得对每一个t∈[m,M],直线y=t与曲线y=f(x),x∈[1,2]都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
【答案】分析:(1)对f(x)进行求导,令f′(x)=0,求出极值点,利用导数研究函数的单调性和极值;
(2)根据(1)的条件,函数f(x)的增区间为(0,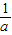 ),减区间为(
),减区间为(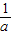 ,+∞),因为
,+∞),因为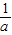 与1,2大小不知道,所以对其进行讨论,分情况求出函数f(x)在[1,2]上的最小值;
与1,2大小不知道,所以对其进行讨论,分情况求出函数f(x)在[1,2]上的最小值;
(3)把a= 代入函数f(x)求出去单调区间,再求出去最值,假设存在,我们可以取f(x)的最小值和最大值组成一个区间,并对其进行验证;
代入函数f(x)求出去单调区间,再求出去最值,假设存在,我们可以取f(x)的最小值和最大值组成一个区间,并对其进行验证;
解答:解:(1)∵f′(x)=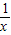 -a=
-a=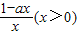 ,
,
∴当a≤0时,f′(x)=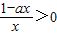 ,即函数f(x)的增区间为(0,+∞),此时f(x)无极值点;
,即函数f(x)的增区间为(0,+∞),此时f(x)无极值点;
当a>0时,令f′(x)=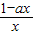 =0得,x=
=0得,x=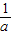 >0.列表如下:
>0.列表如下:
由上表知:函数f(x)的极值点为x=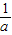 ,且在该极值点处有极大值为f(
,且在该极值点处有极大值为f(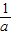 )=-lna-1.…(4分)
)=-lna-1.…(4分)
(2)由(1)知:当a>0时,函数f(x)的增区间为(0,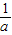 ),减区间为(
),减区间为(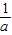 ,+∞).
,+∞).
①若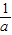 ≤1即a≥1时,函数f(x)在区间[1,2]上为减函数,所以(f(x))min=f(2)=ln2-2a,;
≤1即a≥1时,函数f(x)在区间[1,2]上为减函数,所以(f(x))min=f(2)=ln2-2a,;
②若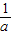 ≥2,即0<a≤
≥2,即0<a≤ 时,函数f(x)在区间[1,2]上为增函数,所以(f(x))min=f(1)=-a,;
时,函数f(x)在区间[1,2]上为增函数,所以(f(x))min=f(1)=-a,;
③若1<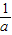 <2,即
<2,即 <a<1时,函数f(x)在区间(1,
<a<1时,函数f(x)在区间(1,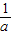 )上为增函数,在区间(
)上为增函数,在区间(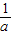 ,2)为减函数,
,2)为减函数,
又f(2)-f(1)=ln2-a,所以,当 <a<ln2时,(f(x))min=f(1)=-a,;
<a<ln2时,(f(x))min=f(1)=-a,;
当ln2≤a<1时,(f(x))min=f(2)=ln2-2a,
综上可知:当0<a<ln2时,(f(x))min=f(1)=-a,;
当a≥ln2时,(f(x))min=f(2)=ln2-2a,
(3)当a= 时,由(2)知函数f(x)在区间(1,
时,由(2)知函数f(x)在区间(1, )上为增函数,在区间(
)上为增函数,在区间( ,2)为减函数,
,2)为减函数,
所以(f(x))min=f( )=ln
)=ln -1,又f(2)-f(1)=ln2-
-1,又f(2)-f(1)=ln2- <0,所以,
<0,所以,
(f(x))min=f(2)=ln2- .
.
故函数y=f(x),x∈[1,2]的值域为[ln2- ,ln
,ln -1].
-1].
据此可得,若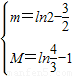 ,相对每一个t∈[m,M],直线y=t与曲线y=f(x),x∈[1,2]都有公共点;
,相对每一个t∈[m,M],直线y=t与曲线y=f(x),x∈[1,2]都有公共点;
并且对每一个t∈(-∞,m)∪(M,+∞),直线y=t与曲线y=f(x),x∈[1,2]都没有公共点.
综上,当a= 时,存在最小的实数m=ln2-
时,存在最小的实数m=ln2- ,最大的实数M=ln
,最大的实数M=ln -1,使得对每一个t∈[m,M],直线y=t与曲线y=f(x),x∈[1,2]都有公共点. …(14分)
-1,使得对每一个t∈[m,M],直线y=t与曲线y=f(x),x∈[1,2]都有公共点. …(14分)
点评:此题主要考查函数、导数等基础知识,考查推理论证能力和抽象概括能力、运算求解能力,考查函数与方程思想,化归和转化思想,分类与整合思想.其中问题(3)是一个存在性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.
(2)根据(1)的条件,函数f(x)的增区间为(0,
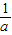 ),减区间为(
),减区间为(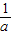 ,+∞),因为
,+∞),因为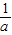 与1,2大小不知道,所以对其进行讨论,分情况求出函数f(x)在[1,2]上的最小值;
与1,2大小不知道,所以对其进行讨论,分情况求出函数f(x)在[1,2]上的最小值;(3)把a=
 代入函数f(x)求出去单调区间,再求出去最值,假设存在,我们可以取f(x)的最小值和最大值组成一个区间,并对其进行验证;
代入函数f(x)求出去单调区间,再求出去最值,假设存在,我们可以取f(x)的最小值和最大值组成一个区间,并对其进行验证;解答:解:(1)∵f′(x)=
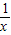 -a=
-a=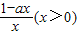 ,
,∴当a≤0时,f′(x)=
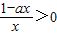 ,即函数f(x)的增区间为(0,+∞),此时f(x)无极值点;
,即函数f(x)的增区间为(0,+∞),此时f(x)无极值点;当a>0时,令f′(x)=
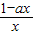 =0得,x=
=0得,x=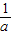 >0.列表如下:
>0.列表如下:| x | (0,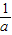 ) ) | 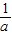 | (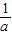 ,+∞), ,+∞), |
| f′(x) | + | - | |
| f(x) | 单调增 | 极大值 | 单调减 |
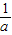 ,且在该极值点处有极大值为f(
,且在该极值点处有极大值为f(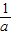 )=-lna-1.…(4分)
)=-lna-1.…(4分)(2)由(1)知:当a>0时,函数f(x)的增区间为(0,
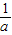 ),减区间为(
),减区间为(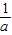 ,+∞).
,+∞).①若
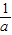 ≤1即a≥1时,函数f(x)在区间[1,2]上为减函数,所以(f(x))min=f(2)=ln2-2a,;
≤1即a≥1时,函数f(x)在区间[1,2]上为减函数,所以(f(x))min=f(2)=ln2-2a,;②若
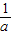 ≥2,即0<a≤
≥2,即0<a≤ 时,函数f(x)在区间[1,2]上为增函数,所以(f(x))min=f(1)=-a,;
时,函数f(x)在区间[1,2]上为增函数,所以(f(x))min=f(1)=-a,;③若1<
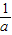 <2,即
<2,即 <a<1时,函数f(x)在区间(1,
<a<1时,函数f(x)在区间(1,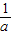 )上为增函数,在区间(
)上为增函数,在区间(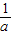 ,2)为减函数,
,2)为减函数,又f(2)-f(1)=ln2-a,所以,当
 <a<ln2时,(f(x))min=f(1)=-a,;
<a<ln2时,(f(x))min=f(1)=-a,;当ln2≤a<1时,(f(x))min=f(2)=ln2-2a,
综上可知:当0<a<ln2时,(f(x))min=f(1)=-a,;
当a≥ln2时,(f(x))min=f(2)=ln2-2a,
(3)当a=
 时,由(2)知函数f(x)在区间(1,
时,由(2)知函数f(x)在区间(1, )上为增函数,在区间(
)上为增函数,在区间( ,2)为减函数,
,2)为减函数,所以(f(x))min=f(
 )=ln
)=ln -1,又f(2)-f(1)=ln2-
-1,又f(2)-f(1)=ln2- <0,所以,
<0,所以,(f(x))min=f(2)=ln2-
 .
.故函数y=f(x),x∈[1,2]的值域为[ln2-
 ,ln
,ln -1].
-1].据此可得,若
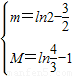 ,相对每一个t∈[m,M],直线y=t与曲线y=f(x),x∈[1,2]都有公共点;
,相对每一个t∈[m,M],直线y=t与曲线y=f(x),x∈[1,2]都有公共点;并且对每一个t∈(-∞,m)∪(M,+∞),直线y=t与曲线y=f(x),x∈[1,2]都没有公共点.
综上,当a=
 时,存在最小的实数m=ln2-
时,存在最小的实数m=ln2- ,最大的实数M=ln
,最大的实数M=ln -1,使得对每一个t∈[m,M],直线y=t与曲线y=f(x),x∈[1,2]都有公共点. …(14分)
-1,使得对每一个t∈[m,M],直线y=t与曲线y=f(x),x∈[1,2]都有公共点. …(14分)点评:此题主要考查函数、导数等基础知识,考查推理论证能力和抽象概括能力、运算求解能力,考查函数与方程思想,化归和转化思想,分类与整合思想.其中问题(3)是一个存在性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

练习册系列答案
相关题目