题目内容
设直线l过点P(-3,3),且倾斜角为
π
(1)写出直线l的参数方程;
(2)设此直线与曲线C:
(θ为参数)交A、B两点,求|PA|•|PB|
| 5 |
| 6 |
(1)写出直线l的参数方程;
(2)设此直线与曲线C:
|
分析:(1)根据直线的参数方程的特征及参数的几何意义,直接写出直线的参数方程.
(2)设点A,B的坐标分别为A(-3-
t1,3+
t1),B(2-
t1,3+
t1).把直线L的参数方程代入圆的椭圆的方程4x2+y2=16整理得到t2+(12
+3)t+
=0,由根与系数的关系及t的几何意义可知|PA||PB|=|t1||t2|,从而求得结果.
(2)设点A,B的坐标分别为A(-3-
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 116 |
| 13 |
解答:解:(1)由于过点(a,b) 倾斜角为α 的直线的参数方程为
(t是参数),
∵直线l经过点P(-3,3),倾斜角α=
,故直线的参数方程是
(t是参数).…(5分)
(2)因为点A,B都在直线l上,所以可设它们对应的参数为t1和t1,则点A,B的坐标分别为A(-3-
t1,3+
t1),B(2-
t1,3+
t1).
把直线L的参数方程代入椭圆的方程4x2+y2=16整理得到t2+(12
+3)t+
=0①,…(8分)
因为t1和t2是方程①的解,从而t1t2=
,
由t的几何意义可知|PA||PB|=|t1||t2|=
. …(10分)
即|PA|•|PB|=
.
|
∵直线l经过点P(-3,3),倾斜角α=
| 5π |
| 6 |
|
(2)因为点A,B都在直线l上,所以可设它们对应的参数为t1和t1,则点A,B的坐标分别为A(-3-
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
把直线L的参数方程代入椭圆的方程4x2+y2=16整理得到t2+(12
| 3 |
| 116 |
| 13 |
因为t1和t2是方程①的解,从而t1t2=
| 116 |
| 13 |
由t的几何意义可知|PA||PB|=|t1||t2|=
| 116 |
| 13 |
即|PA|•|PB|=
| 116 |
| 13 |
点评:本题主要考查直线的参数方程,以及直线的参数方程中参数的几何意义,直线和圆的位置关系的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
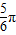
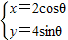 (θ为参数)交A、B两点,求|PA|•|PB|
(θ为参数)交A、B两点,求|PA|•|PB|