题目内容

（2012•泉州模拟）函数的图象与方程的曲线有着密切的联系，如把抛物线y2=x的图象绕原点沿逆时针方向旋转90°就得到函数y=x2的图象．若把双曲线
x2
3
-y2=1绕原点按逆时针方向旋转一定角度θ后，能得到某一个函数的图象，则旋转角θ可以是（　　）
分析：确定双曲线的渐近线方程，求出倾斜角，即可得到结论．
解答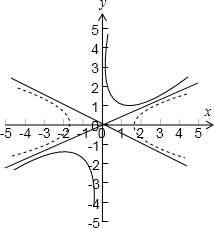：解：双曲线
x2
3
-y2=1的渐近线方程为y=±
3
3
x，其倾斜角为30°或150°
在双曲线
x2
3
-y2=1上取点（m，n），关于y=
3
3
x对称点的坐标为（x，y），则
y-n
x-m
=-
3
n+y
2
=
3
3
×
m+x
2
，∴
m=
3
y
2
+
x
2
n=
3
x
2
-
y
2

∵
m2
3
-n2=1，∴y=
3
2x
此时，是一个函数的图象
故把双曲线
x2
3
-y2=1绕原点按逆时针方向旋转60°时，双曲线方程为y=
3
2x
，双曲线的渐近线方程为x=0，与y=
3
3
x，图象如图所示
故选C．
点评：本题考查双曲线的标准方程与性质，考查图象变换，属于中档题．
练习册系列答案
相关题目
（2012•泉州模拟）已知f0(x)=x•ex，f1（x）=f′0（x），f2（x）=f′1（x），…，fn（x）=f′n-1（x）（n∈N*）．
（Ⅰ）请写出fn（x）的表达式（不需证明）；
（Ⅱ）设fn（x）的极小值点为Pn（xn，yn），求yn；
（Ⅲ）设gn(x)=-x2-2(n+1)x-8n+8，gn（x）的最大值为a，fn（x）的最小值为b，试求a-b的最小值．
（2012•泉州模拟）下列函数中，既是偶函数，且在区间（0，+∞）内是单调递增的函数是（　　）
（2012•泉州模拟）已知集合A={1，2，3}，B={x|x2-x-2=0，x∈R}，则A∩B为（　　）
（2012•泉州模拟）设函数f（x）=ax2+lnx．
（Ⅰ）当a=-1时，求函数y=f（x）的图象在点（1，f（1））处的切线方程；
（Ⅱ）已知a＜0，若函数y=f（x）的图象总在直线y=-
12
的下方，求a的取值范围；
（Ⅲ）记f′（x）为函数f（x）的导函数．若a=1，试问：在区间[1，10]上是否存在k（k＜100）个正数x1，x2，x3…xk，使得f′（x1）+f'（x2）+f′（x3）+…+f′（xk）≥2012成立？请证明你的结论．
（2012•泉州模拟）设函数y=f（x）的定义域为D，若对于任意x1，x2∈D且x1+x2=2a，恒有f（x1）+f（x2）=2b，则称点（a，b）为函数y=f（x）图象的对称中心．研究并利用函数f（x）=x3-3x2-sin（πx）的对称中心，可得f(
1
2012
)+f(
2
2012
)+…+f(
4022
2012
)+f(
4023
2012
)=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网