题目内容
已知函数f(x)=cos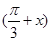 cos
cos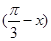 -sin xcos x+
-sin xcos x+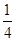
(1)求函数f(x)的最小正周期和最大值;
(2)求函数f(x)单调递增区间.
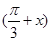 cos
cos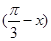 -sin xcos x+
-sin xcos x+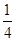
(1)求函数f(x)的最小正周期和最大值;
(2)求函数f(x)单调递增区间.
(1)最小正周期为T=π,最大值为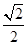 (2)
(2)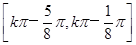 ,k∈Z
,k∈Z
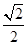 (2)
(2)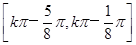 ,k∈Z
,k∈Z(1)∵f(x)=cos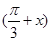 cos
cos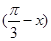 -
-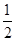 sin 2x+
sin 2x+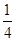
=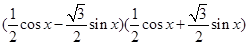 -
-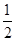 sin 2x+
sin 2x+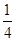
=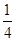 cos2x-
cos2x-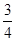 sin2x-
sin2x-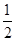 sin 2x+
sin 2x+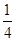
=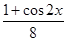 -
-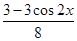 -
-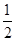 sin 2x+
sin 2x+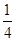
=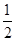 (cos 2x-sin 2x)=
(cos 2x-sin 2x)=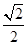 cos
cos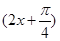 ,
,
函数f(x)的最小正周期为T=π,
函数f(x)的最大值为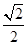 .
.
(2)由2kπ-π≤2x+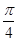 ≤2kπ,k∈Z,
≤2kπ,k∈Z,
得kπ-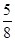 π≤x≤kπ-
π≤x≤kπ-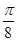 ,k∈Z,
,k∈Z,
故函数f(x)的单调递增区间为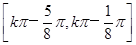 ,k∈Z.
,k∈Z.
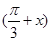 cos
cos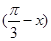 -
-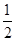 sin 2x+
sin 2x+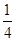
=
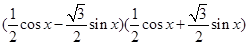 -
-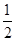 sin 2x+
sin 2x+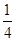
=
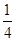 cos2x-
cos2x-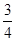 sin2x-
sin2x-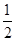 sin 2x+
sin 2x+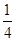
=
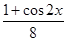 -
-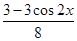 -
-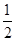 sin 2x+
sin 2x+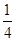
=
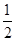 (cos 2x-sin 2x)=
(cos 2x-sin 2x)=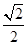 cos
cos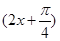 ,
,函数f(x)的最小正周期为T=π,
函数f(x)的最大值为
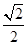 .
.(2)由2kπ-π≤2x+
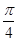 ≤2kπ,k∈Z,
≤2kπ,k∈Z,得kπ-
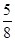 π≤x≤kπ-
π≤x≤kπ-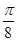 ,k∈Z,
,k∈Z,故函数f(x)的单调递增区间为
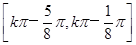 ,k∈Z.
,k∈Z.
练习册系列答案
相关题目
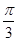 对称,且f
对称,且f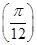 =0,则ω的最小值为( ).
=0,则ω的最小值为( ).
 的最小正周期是
的最小正周期是 ,则
,则 .
.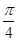 时,函数f(x)=Asin (x+φ)(A>0)取得最小值,则函数y=f
时,函数f(x)=Asin (x+φ)(A>0)取得最小值,则函数y=f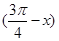 是( ).
是( ).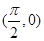 对称
对称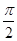 对称
对称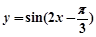 的图象可以由
的图象可以由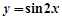 的图象向右平移
的图象向右平移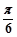 个单位长度得到;
个单位长度得到;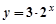 的图象可以由函数
的图象可以由函数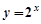 的图象向左或向右平移得到;
的图象向左或向右平移得到;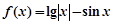 的零点个数为
的零点个数为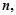 则
则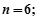
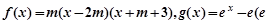 是自然对数的底数),如果对于任意
是自然对数的底数),如果对于任意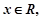 总有
总有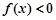 或
或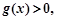 且存在
且存在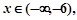 使得
使得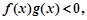 则实数
则实数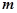 的取值范围是
的取值范围是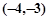 .
. 的最小正周期为 .
的最小正周期为 . 的最小正周期为 .
的最小正周期为 .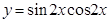 的最小正周期是 .
的最小正周期是 .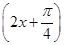 的最小正周期为 ________.
的最小正周期为 ________.