题目内容
(本小题满分12分)甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.射击环数的频率分布条形图如下:
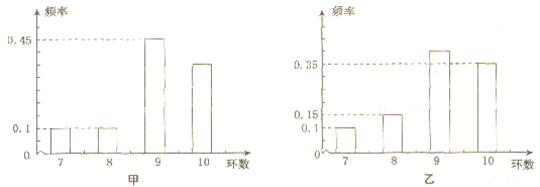
若将频率视为概率,回答下列问题.(Ⅰ)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率; (Ⅱ)若甲、乙两运动员各自射击1次,ξ表示这2次射击中击中9环以上(含9环)的次数,求ξ的分布列及Eξ.
(I)p= 0.992(II)Eξ=1.55.
解析:
解法一:(Ⅰ)甲运动员击中10环的概率是:1一0.1—0.1—0.45=0.35.
设事件A表示“甲运动员射击一次,恰好命中9环以上(含9环,下同)”, 则P(A)=0.35+0.45=0.8.
事件“甲运动员在3次射击中,至少1次击中9环以上”包含三种情况:恰有1次击中9环以上,概率为p1=C![]() ·0.81·(1-0.8)2=0.096; 恰有2次击中9环以上,概率为p2=C
·0.81·(1-0.8)2=0.096; 恰有2次击中9环以上,概率为p2=C![]() ·0.82·(1-0.8)1=0.384;
·0.82·(1-0.8)1=0.384;
恰有3次击中9环以上,概率为p3=C![]() ·0.83·(1-0.8)0=0.512. 因为上述三个事件互斥,所以甲运动员射击3次,至少1次击中9环以上的概率p= p1+ p2+ p3=0.992.
·0.83·(1-0.8)0=0.512. 因为上述三个事件互斥,所以甲运动员射击3次,至少1次击中9环以上的概率p= p1+ p2+ p3=0.992.
(Ⅱ)记“乙运动员射击1次,击中9环以上”为事件B, 则P(B)=1—0.1—0.15=0.75.
因为![]() 表示2次射击击中9环以上的次数,所以
表示2次射击击中9环以上的次数,所以![]() 的可能取值是0,1,2.
的可能取值是0,1,2.
因为P(![]() =2)=0.8·0.75=0.6; P(
=2)=0.8·0.75=0.6; P(![]() =1)=0.8·(1-0.75)+(1-0.8)·0.75=0.35;
=1)=0.8·(1-0.75)+(1-0.8)·0.75=0.35;
P(![]() =0)=(1-0.8)·(1-0.75)=0.05. 所以
=0)=(1-0.8)·(1-0.75)=0.05. 所以![]() 的分布列是
的分布列是
| ξ | 0 | 1 | 2 |
| P | 0.05 | 0.35 | 0.6 |
所以Eξ=0×0.05+1×0.35+2×0.6=1.55.
解法二:
(Ⅰ)设事件A表示“甲运动员射击一次,恰好命中9环以上”(含9环,下同),
则P(A)=1-0.1-0.1=0.8.
甲运动员射击3次,均未击中9环以上的概率为
P0=C![]() ·0.80·(1-0.8)3=0.008.
·0.80·(1-0.8)3=0.008.
所以甲运动员射击3次,至少1次击中9环以上的概率P=1-P0=0.992.
(Ⅱ)同解法一.

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案