题目内容
(本小题满分15分)
已知函数 .
.
(Ⅰ)
若曲线 在点
在点 处的切线
处的切线 与曲线
与曲线 有且只有一个公共点,求
有且只有一个公共点,求 的值;
的值;
(Ⅱ) 求证:函数 存在单调递减区间
存在单调递减区间 ,并求出单调递减区间的长度
,并求出单调递减区间的长度 的取值范围.
的取值范围.
【答案】
(Ⅰ)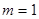 .(Ⅱ)以函数
.(Ⅱ)以函数 的递减区间长度
的递减区间长度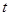 的取值范围是
的取值范围是 .
.
【解析】本试题主要考查了导数在研究函数中 的运用。
(1)先求解函数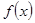 的定义域为
的定义域为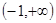 ,函数导数
,函数导数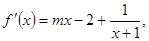

所以曲线 在点
在点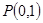 处的切线方程为:
处的切线方程为: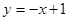
因为切线与曲线有唯一的公共点,
所以方程 有且只有一个实数解,显然
有且只有一个实数解,显然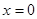 是方程的一个解.
是方程的一个解.
构造函数令 ,则
,则
对参数m讨论得到结论。
(2))因为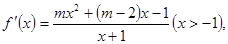
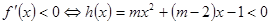 .
.
因为 且对称轴为
且对称轴为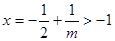 ,
,
 ,
,
所以方程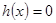 在
在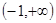 内有两个不同实根
内有两个不同实根 ,
,
结合韦达定理得到结论。
解:(Ⅰ)函数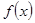 的定义域为
的定义域为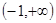 ,
,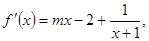

所以曲线 在点
在点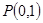 处的切线方程为:
处的切线方程为: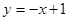
因为切线与曲线有唯一的公共点,
所以方程 有且只有一个实数解,显然
有且只有一个实数解,显然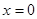 是方程的一个解.
是方程的一个解.
令 ,则
,则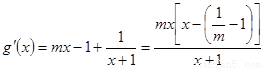
①当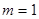 时,
时, ,
,
所以 在
在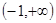 上单调递增,即
上单调递增,即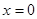 是方程唯一实数解.
是方程唯一实数解.
②当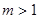 时,由
时,由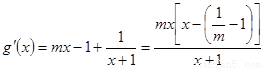 得
得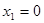 ,
,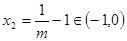 ,
,
在区间 上,
上, ;在区间
;在区间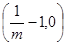 上,
上,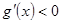 ;
;
所以函数 在
在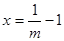 处有极大值
处有极大值 ,且
,且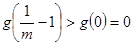 ;
;
而当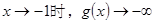 ,因此
,因此 在
在 内也有一个解.
内也有一个解.
即当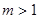 时,不合题目的条件.
时,不合题目的条件.
综上讨论得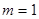 .……………………………………………………………………………8分
.……………………………………………………………………………8分
(Ⅱ)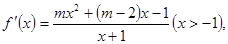
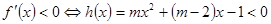 .
.
因为 且对称轴为
且对称轴为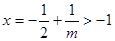 ,
,
 ,
,
所以方程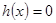 在
在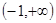 内有两个不同实根
内有两个不同实根 ,
,
即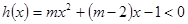 的解集为
的解集为 ,
,
所以函数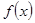 的单调递减区间为
的单调递减区间为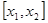 .
.
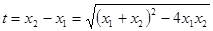

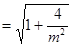
由于 ,所以
,所以
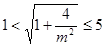 ,
,
所以函数 的递减区间长度
的递减区间长度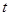 的取值范围是
的取值范围是 .……………………15分
.……………………15分

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目

 的单调区间;
的单调区间; ,试分别解答以下两小题.
,试分别解答以下两小题. 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 是两个不相等的正数,且
是两个不相等的正数,且 ,求证:
,求证: .
. 、
、 分别为椭圆
分别为椭圆 :
: 的
的  :
: 的焦点,
的焦点, 是
是 。
。 :
: ,过点P的动直线
,过点P的动直线 与圆
与圆 ,
, (
( 且
且 )。求证:点Q总在某定直线上。
)。求证:点Q总在某定直线上。
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,过
,过 与椭圆相交于A、B两点。
与椭圆相交于A、B两点。 ,且
,且 ,求椭圆的离心率;
,求椭圆的离心率; 求
求 的最大值和最小值。
的最大值和最小值。
 在定义域内存在区间
在定义域内存在区间 ,满足
,满足 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出 ;若不是,说明理由;
;若不是,说明理由; 为“优美函数”,求实数
为“优美函数”,求实数 的取值范围.
的取值范围.