题目内容
对于任意定义在区间D上的函数f（x），若实数x0∈D满足f（x0）=x0，则称x0为函数f（x）在D上的一个不动点．
（1）求函数f(x)=2x+
-2在（0，+∞）上的不动点；
（2）若函数f(x)=2x+
+a，在（0，+∞）上没有不动点，求实数a的取值范围．
（1）求函数f(x)=2x+
| 1 |
| x |
（2）若函数f(x)=2x+
| a |
| x |
（1）设函数f(x)=2x+
-2在（0，+∞）上的不动点为x0
则2x0+
-2= x0，且x0∈（0，+∞）
∴x0=1
（2）若函数f(x)=2x+
+a，在（0，+∞）上没有不动点
则2x+
+a=x在x∈（0，+∞）没有实数解
∴x2+ax+a=0在x∈（0，+∞）没有实数解
∴△=a2-4a＜0或
∴0＜a＜4或a≥4
| 1 |
| x |
则2x0+
| 1 |
| x0 |
∴x0=1
（2）若函数f(x)=2x+
| a |
| x |
则2x+
| a |
| x |
∴x2+ax+a=0在x∈（0，+∞）没有实数解
∴△=a2-4a＜0或
|
∴0＜a＜4或a≥4
练习册系列答案
相关题目
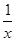+a在区间(0，+∞)上没有不动点，则实数a取值范围是_______.
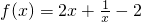在（0，+∞）上的不动点；
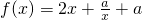，在（0，+∞）上没有不动点，求实数a的取值范围．