题目内容
直线l1：x+ay+6=0与l2：（a-2）x+3y+2a=0平行，则a的值等于（ ）
| A、-1或3 | B、1或3 |
| C、-3 | D、-1 |
考点：直线的一般式方程与直线的平行关系
专题：直线与圆
分析：直接利用两直线平行的充要条件，列出方程求解，解得a的值．
解答：
解：因为两条直线平行，两直线的斜率都存在，故它们的斜率相等，
由
=
≠
，解得：a=-1，
故选：D．
由
| 1 |
| a-2 |
| a |
| 3 |
| 6 |
| 2a |
故选：D．
点评：本题考查两直线平行的条件，要注意特殊情况即直线斜率不存在的情况，要进行检验．
练习册系列答案
相关题目
设a=
(3x2-2x)dx，则a=（ ）
| ∫ | 2 1 |
| A、12 | B、4 | C、-12 | D、-4 |
函数y=1-2cos（
x）的周期为（ ）
| π |
| 2 |
| A、2π | B、1 | C、4 | D、2 |
已知△ABC中，AB=6，BC=4，∠B=60°，则△ABC的面积为（ ）
| A、6 | ||
| B、9 | ||
C、6
| ||
D、9
|
以下4组函数中，表示同一函数的是（ ）
A、f（x）=
| ||||||
B、f（x）=|x|，g（x）=
| ||||||
C、f（x）=
| ||||||
D、f（x）=
|
若a=ln2，b=ln3，c=lg0.1，则a，b，c的大小顺序是（ ）
| A、a＞b＞c |
| B、c＞b＞a |
| C、b＞a＞c |
| D、b＞c＞a |
已知sin(
+α)=
，则cosα的值是（ ）
| π |
| 2 |
| 3 |
| 5 |
A、-
| ||
B、±
| ||
C、
| ||
D、
|
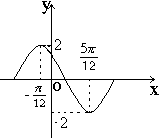函数y=Acos（ωx+φ）在一个周期内的图象如下，此函数的解析式为（ ）A、y=2cos（2x+
| ||||
B、y=2cos（2x-
| ||||
C、y=2cos（
| ||||
D、y=2cos（2x+
|