题目内容
函数y=
x2
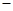㏑x的单调递减区间为（ ）
A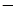．（ 1,1] | B．（0,1] | C．[1，+∞） | D．（0，+∞） |
B
解析试题分析：∵y=
x2 lnx的定义域为（0，+∞），y′=
，∴由y′≤0得：0＜x≤1，∴函数y=x2 lnx的单调递减区间为（0，1]，故选B .
考点：利用导数研究函数的单调性.
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
曲线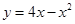
上两点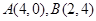
，若曲线上一点
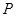处的切线恰好平行于弦
，则点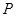的坐标为（ ）
| A．(1,3） | B．(3,3） | C．(6,-12） | D．(2,4） |
函数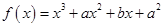
在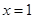
时有极值10，则
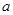的值为（ ）
| A．-3或4 | B．4 | C．-3 | D．3或 4 |
设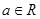
,函数
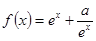的导函数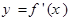
是奇函数，若曲线
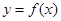的一条切线的斜率为
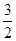，则切点的横坐标是（ ）
A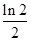． | B． | C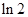． | D． |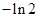
设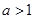
，若曲线
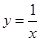与直线
，
，
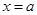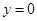所围成封闭图形的面积为2，则
（ ）
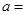| A．2 | B．e | C．2e | D． |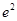
函数y=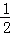
x2﹣lnx的单调递减区间为（ ）
| A．（﹣1，1] | B．（0，1] |
| C．[1，+∞） | D．（0，+∞） |
已知函数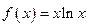
．若直线l过点(0，－1)，并且与曲线y=f(x)相切，则直线l的方程为( )
| A．x+y－1=0 |
| B．x－y－1=0 |
| C．x+y+1=0 |
| D．x－y+1=0 |
已知二次函数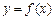
的图象如图所示，则它与
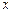轴所围图形的面积为（ ）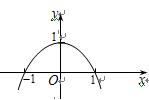
A． |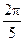
B． |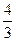
C． |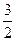
D． |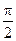
已知函数
在区间[－1，2]上是减函数，那么b+c( )
A．有最大值 |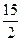
| B．有最大值－ |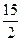
| C．有最小值 |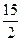
| D．有最小值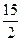－ |