题目内容
已知向量
=(0,2),
=(2,0),
=(
cosα,
sinα),则
与
夹角的取值范围是( )
| OA |
| OB |
| BC |
| 2 |
| 2 |
| OA |
| OC |
分析:由题知点C在以B(2,0)为圆心,为半径的圆上,所以本题应采用数形结合来解题,由图来分析其夹角的最大最小值点
解答: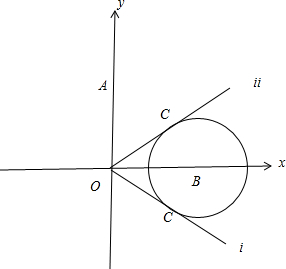 解:∵
解:∵
=
+
=(2,0)+(
cosα,
sinα)=(2+
cosα,
sinα)
令x=2+
cosα,y=
sinα,则(x-2)2+y2=2
则C在以M(2,0)为圆心以
为半径的圆上
设直线AC:y=kx,当直线AC与圆B相切时,由
=
可得k=±1
当C在如图所示的i位置时,夹角最大,此时夹角
+
=
当C在如图所示的ii位置时,夹角最小,此时夹角
-
=
夹角
≤α≤
故选C
 解:∵
解:∵| OC |
| OB |
| BC |
| 2 |
| 2 |
| 2 |
| 2 |
令x=2+
| 2 |
| 2 |
则C在以M(2,0)为圆心以
| 2 |
设直线AC:y=kx,当直线AC与圆B相切时,由
| |2k| | ||
|
| 2 |
当C在如图所示的i位置时,夹角最大,此时夹角
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
当C在如图所示的ii位置时,夹角最小,此时夹角
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
夹角
| π |
| 4 |
| 3π |
| 4 |
故选C
点评:本题考查向量的坐标运算及向量的数量积与夹角,解题的关键是求出C的轨迹,结合圆的性质进行求解,是一道考查基本功的题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目