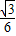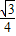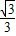题目内容
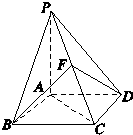
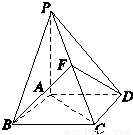
 如图所示,已知点P为菱形ABCD外一点,且PA⊥面ABCD,PA=AD=AC,点F为PC中点,则二面角CBFD的正切值为( )
如图所示,已知点P为菱形ABCD外一点,且PA⊥面ABCD,PA=AD=AC,点F为PC中点,则二面角CBFD的正切值为( )分析:如图所示,建立空间直角坐标系,利用两个平面的法向量的夹角公式即可得出二面角的余弦,进而利用平方关系及商数关系即可得出.
解答:解:如图所示,连接AC,AC∩BD=O,连接OF,
以O为原点,OB、OC、OF所在直线为x,y,z距离空间直角坐标系,
不妨设PA=AD=AC=1,则BD=
.
则B(
,0,0),F(0,0,
),C(0,
,0),D(-
,0,0).
=(0,
,0)且为平面BOF的一个法向量,由
=(-
,
,0),
=(
,0,-
).
设平面BCF的法向量为
=(x,y,z),则
,
不妨取x=1,则y=
=z.∴
=(1,
,
).
∴cos<
,
>=
=
,sin<
,
>=
,
∴tan<
,
>=
.
故选D.
以O为原点,OB、OC、OF所在直线为x,y,z距离空间直角坐标系,
不妨设PA=AD=AC=1,则BD=
| 3 |
则B(
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| OC |
| 1 |
| 2 |
| BC |
| ||
| 2 |
| 1 |
| 2 |
| FB |
| ||
| 2 |
| 1 |
| 2 |
设平面BCF的法向量为
| n |
|
不妨取x=1,则y=
| 3 |
| n |
| 3 |
| 3 |
∴cos<
| n |
| OC |
| ||||
|
|
| ||
| 7 |
| n |
| OC |
2
| ||
| 7 |
∴tan<
| n |
| OC |
2
| ||
| 3 |
故选D.
点评:熟练掌握通过建立空间直角坐标系利用两个平面的法向量的夹角公式即可得出二面角的余弦的方法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
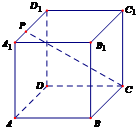 如图所示,已知点P是正方体ABCD-A1B1C1D1的棱A1D1上的一个动点,设异面直线AB与CP所成的角为α,则cosα的最小值是
如图所示,已知点P是正方体ABCD-A1B1C1D1的棱A1D1上的一个动点,设异面直线AB与CP所成的角为α,则cosα的最小值是