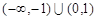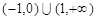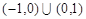题目内容
对于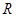 上可导的任意函数
上可导的任意函数 ,若满足
,若满足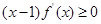 ,则必有( )
,则必有( )
A.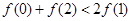 | B.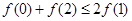 |
C.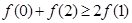 | D.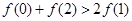 |
C
解析试题分析:依题意,当x≥1时,f′(x)≥0,函数f(x)在(1,+∞)上是增函数;
当x<1时,f′(x)≤0,f(x)在(-∞,1)上是减函数,
故当x=1时f(x)取得最小值,即有f(0)≥f(1),f(2)≥f(1),
∴f(0)+f(2)≥2f(1).故选C.
考点:应用导数研究函数的单调性
点评:简单题,比较函数值的大小问题,常常利用函数的单调性,本题通过分类讨论x的不同取值情况下,导函数的正负,明确函数的单调性,使问题得解。

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
已知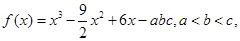 且
且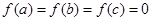 ,现给出如下结论:
,现给出如下结论:
①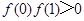 ;②
;②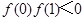 ;③
;③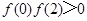 ;④
;④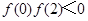 .其中正确结论的序号为:( )
.其中正确结论的序号为:( )
| A.①③ | B.①④ | C.②④ | D.②③ |
若实数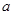 、
、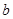 、
、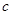 、
、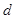 满足
满足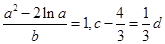 ,则
,则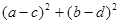 的最小值 为 ( )
的最小值 为 ( )
A.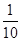 | B.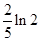 | C.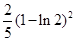 | D.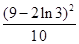 |
已知点P在曲线y=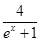 上,
上,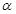 为曲线在点P处的切线的倾斜角,则
为曲线在点P处的切线的倾斜角,则 的取值范围是( )
的取值范围是( )
A.[0,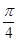 ) ) | B.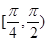 | C.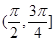 | D.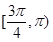 |
已知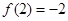 ,
,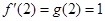 ,
, ,则函数
,则函数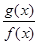 在
在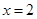 处的导数值为( )
处的导数值为( )
A.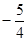 | B.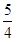 | C. | D. |
曲线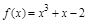 上点
上点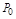 处的切线垂直于直线
处的切线垂直于直线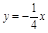 ,则点P0的坐标是( )
,则点P0的坐标是( )
A.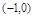 | B.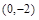 | C.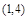 | D.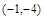 或 或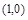 |
设函数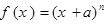 ,其中
,其中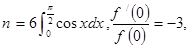 则
则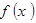 的展开式中
的展开式中 的系数为( )
的系数为( )
| A.-360 | B.360 | C.-60 | D.60 |
函数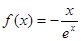 (
(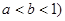 ,则 ( )
,则 ( )
A.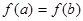 | B.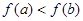 |
C.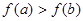 | D.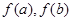 大小关系不能确定 大小关系不能确定 |
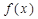 是定义在R上的奇函数,且
是定义在R上的奇函数,且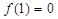 ,当
,当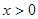 时,有
时,有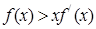 恒成立,则不等式
恒成立,则不等式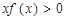 的解集为( )
的解集为( )