题目内容
已知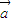 、
、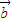 为两个非零向量,有以下命题:①
为两个非零向量,有以下命题:①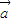 2=
2=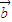 2 ②
2 ②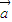 •
•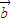 =
=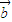 2 ③|
2 ③| |=|
|=|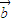 |且
|且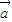 ∥
∥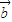 ,其中可以作
,其中可以作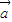 =
=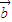 的必要但不充分条件的命题的( )
的必要但不充分条件的命题的( )A.②
B.①③
C.②③
D.①②③
【答案】分析:根据向量相等的定义:向量相等需要同时满足两个条件,大小(模)相等,反向相反,对题目中的三个结论逐一进行判断,分析即可得到答案.
解答:解:两个向量相等,表示两个向量大小相等,方向相同
①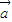 2=
2=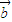 2?|
2?|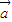 |=|
|=| |,|
|,|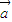 |=|
|=|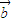 |只能表示两个向量的大小相等,但方向不一定相同,
|只能表示两个向量的大小相等,但方向不一定相同,
故| |=|
|=| |⇒
|⇒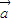 =
=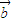 为假命题,
为假命题,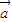 =
= ⇒|
⇒| |=|
|=| |为真命题,
|为真命题,
故①可以做为a=b的必要不充分条件
②若 2=
2=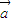 •
•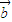 ,则:
,则: •(
•( 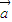 -
-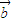 )=0,则表示
)=0,则表示 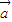 与(
与(  -
-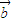 )垂直,此时
)垂直,此时 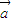 =
= 不一定成立,
不一定成立,
但当 =
= 时,
时, 2=
2=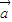 •
•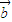 一定成立,故②也可以做为a=b的必要不充分条件;
一定成立,故②也可以做为a=b的必要不充分条件;
③| |=|
|=|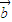 |且
|且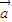 ∥
∥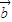 ,只能表示两个向量的大小相等,但方向不一定相同,
,只能表示两个向量的大小相等,但方向不一定相同,
故| |=|
|=|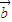 |且
|且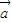 ∥
∥ ,⇒
,⇒ =
=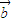 为假命题,
为假命题, =
= ⇒|
⇒|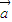 |=|
|=|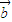 |且
|且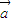 ∥
∥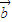 ,为真命题,
,为真命题,
故③可以做为a=b的必要不充分条件
答案为:①②③.
故选D.
点评:本题考查的知识点必要条件、充分条件与充要条件的判断.判断充要条件的方法是:①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.
解答:解:两个向量相等,表示两个向量大小相等,方向相同
①
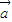 2=
2=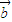 2?|
2?|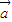 |=|
|=| |,|
|,|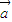 |=|
|=|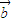 |只能表示两个向量的大小相等,但方向不一定相同,
|只能表示两个向量的大小相等,但方向不一定相同,故|
 |=|
|=| |⇒
|⇒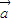 =
=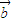 为假命题,
为假命题,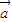 =
= ⇒|
⇒| |=|
|=| |为真命题,
|为真命题,故①可以做为a=b的必要不充分条件
②若
 2=
2=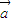 •
•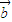 ,则:
,则: •(
•( 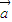 -
-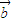 )=0,则表示
)=0,则表示 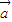 与(
与(  -
-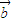 )垂直,此时
)垂直,此时 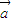 =
= 不一定成立,
不一定成立,但当
 =
= 时,
时, 2=
2=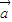 •
•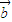 一定成立,故②也可以做为a=b的必要不充分条件;
一定成立,故②也可以做为a=b的必要不充分条件;③|
 |=|
|=|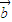 |且
|且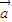 ∥
∥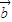 ,只能表示两个向量的大小相等,但方向不一定相同,
,只能表示两个向量的大小相等,但方向不一定相同,故|
 |=|
|=|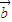 |且
|且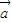 ∥
∥ ,⇒
,⇒ =
=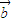 为假命题,
为假命题, =
= ⇒|
⇒|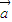 |=|
|=|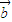 |且
|且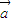 ∥
∥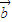 ,为真命题,
,为真命题,故③可以做为a=b的必要不充分条件
答案为:①②③.
故选D.
点评:本题考查的知识点必要条件、充分条件与充要条件的判断.判断充要条件的方法是:①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

练习册系列答案
相关题目
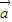 ,
,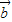 为两个非零向量,则“
为两个非零向量,则“ ”是“
”是“ ”成立的( )
”成立的( ) ,
,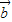 为两个非零向量,则“
为两个非零向量,则“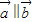 ”是“
”是“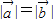 ”成立的( )
”成立的( ) ,
, 为两个非零向量,集合A={x|a1x+b1≥0},集合B={x|a2x+b2≥0},则
为两个非零向量,集合A={x|a1x+b1≥0},集合B={x|a2x+b2≥0},则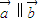 是A=B的 ( )
是A=B的 ( ) ,
, 为两个非零向量,集合A={x|a1x+b1≥0},集合B={x|a2x+b2≥0},则
为两个非零向量,集合A={x|a1x+b1≥0},集合B={x|a2x+b2≥0},则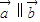 是A=B的 ( )
是A=B的 ( )