题目内容
【题目】已知函数f(x)=ax3+cx+d(a≠0)是R上的奇函数,当x=1时,f(x)取得极值-2.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调区间和极大值;
(3)证明:对任意x1、x2∈(-1,1),不等式|f(x1)-f(x2)|<4恒成立.
【答案】(1)f(x)=x3-3x;(2)f(x)的递增区间是(-∞,-1)和(1,+∞);递减区间为(-1,1).极大值为f(-1)=2;(3)证明见解析.
【解析】试题分析:(1)分析已知条件,函数为奇函数,即![]() ,可得
,可得![]() ,“当x=1时,f(x)取得极值-2”得
,“当x=1时,f(x)取得极值-2”得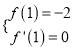 ,可解得
,可解得![]() ;(2)由
;(2)由![]() 确定增区间,由
确定增区间,由![]() 得减区间,从而确定极值点;(3)要证题设命题,只要求出
得减区间,从而确定极值点;(3)要证题设命题,只要求出![]() 在
在![]() 上的最大值和最小值,证明最大值-最小值≤4即可,为此可由第(2)小题的结论很快求得.
上的最大值和最小值,证明最大值-最小值≤4即可,为此可由第(2)小题的结论很快求得.
试题解析:(1)∵f(x)是R上的奇函数,
∴f(-x)=-f(x),
即-ax3-cx+d=-ax3-cx-d,∴d=-d,
∴d=0(或由f(0)=0得d=0).
∴f(x)=ax3+cx,f ′(x)=3ax2+c,
又当x=1时,f(x)取得极值-2,
∴ ,即
,即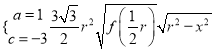 解得
解得![]()
∴f(x)=x3-3x.
(2)f ′(x)=3x2-3=3(x+1)(x-1),令f ′(x)=0,得x=±1,
当-1<x<1时,f ′(x)<0,函数f(x)单调递减;
当x<-1或x>1时,f ′(x)>0,函数f(x)单调递增;
∴函数f(x)的递增区间是(-∞,-1)和(1,+∞);递减区间为(-1,1).
因此,f(x)在x=-1处取得极大值,且极大值为f(-1)=2.
(3)由(2)知,函数f(x)在区间[-1,1]上单调递减,且f(x)在区间[-1,1]上的最大值为M=f(-1)=2.最小值为m=f(1)=-2.∴对任意x1、x2∈(-1,1),
|f(x1)-f(x2)|<M-m=4成立.
即对任意x1、x2∈(-1,1),不等式|f(x1)-f(x2)|<4恒成立.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案【题目】某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下的对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;
(2)求y关于x的线性回归方程。
(3)如果广告费支出为一千万元,预测销售额大约为多少百万元?
参考公式
用最小二乘法求线性回归方程系数公式: ,
, ![]() .
.
【题目】某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
学习积极性一般 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)判断是否有![]() 的把握认为学生的学习积极性与对待班级工作的态度有关系?
的把握认为学生的学习积极性与对待班级工作的态度有关系?
附:  , n=a+b+c+d.
, n=a+b+c+d.
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下表所示:
零件的个数x/个 | 2 | 3 | 4 | 5 |
加工的时间y/h | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
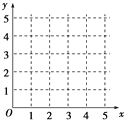
(2)求出y关于x的线性回归方程![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间.