题目内容
设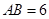 ,在线段
,在线段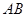 上任取两点(不含两端点),将线段分成了三条线段.
上任取两点(不含两端点),将线段分成了三条线段.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形的概率.
(1)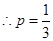 ; (2)
; (2)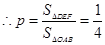 .
.
【解析】1)本题是一个古典概型,若分成的三条线段的长度均为正整数,则三条线段的长度的所有可能为:1,1,4;1,2,3;2,2,2共3种情况,其中只有三条线段为2,2,2时能构成三角形,得到概率.
(2)本题是一个几何概型,设出变量,写出全部结果所构成的区域,和满足条件的事件对应的区域,注意整理三条线段能组成三角形的条件,做出面积,做比值得到概率

 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案设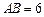 ,在线段
,在线段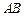 上任取两点C,D(端点
上任取两点C,D(端点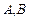 除外),将线段
除外),将线段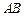 分成三条线段AC,CD,DB.
分成三条线段AC,CD,DB.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数摸拟的方法,来近似计算(Ⅱ)中事件B的概率.
20组随机数如下:
| | 1组 | 2组 | 3组 | 4组 | 5组 | 6组 | 7组 | 8组 | 9组 | 10组 |
| X | 0.52 | 0.36 | 0.58 | 0.73 | 0.41 | 0. 6 6 | 0.05 | 0.32 | 0.38 | 0.73 |
| Y | 0.76 | 0.39 | 0.37 | 0.01 | 0.04 | 0.28 | 0.03 | 0.15 | 0.14 | 0 .86 .86 |
| | 11组 | 12组 | 13组 | 14组 | 15组 | 16组 | 17组 | 18组 | 19组 | 20组 |
| X | 0.67 | 0.47 | 0.58 | 0.21 | 0.54 | 0. 64 64 | 0.36 | 0.35 | 0.95 | 0.14 |
| Y | 0.41 | 0.54 | 0.51 | 0.37 | 0.31 | 0.23 | 0.56 | 0.89 | 0.17 | 0.03 |
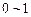 之间的均匀随机数,Y也是
之间的均匀随机数,Y也是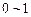 之间的均匀随机
之间的均匀随机 数)
数) 设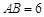 ,在线段
,在线段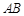 上任取两点C,D(端点
上任取两点C,D(端点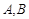 除外),将线段
除外),将线段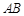 分成三条线段AC,CD,DB.
分成三条线段AC,CD,DB.
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形(称事件A)的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形(称事件B)的概率;
(3)根据以下用计算机所产生的20组随机数,试用随机数摸拟的方法,来近似计算(Ⅱ)中事件B的概率.
20组随机数如下:
|
|
1组 |
2组 |
3组 |
4组 |
5组 |
6组 |
7组 |
8组 |
9组 |
10组 |
|
X |
0.52 |
0.36 |
0.58 |
0.73 |
0.41 |
0. 6 |
0.05 |
0.32 |
0.38 |
0.73 |
|
Y |
0.76 |
0.39 |
0.37 |
0.01 |
0.04 |
0.28 |
0.03 |
0.15 |
0.14 |
0.86 |
|
|
11组 |
12组 |
13组 |
14组 |
15组 |
16组 |
17组 |
18组 |
19组 |
20组 |
|
X |
0.67 |
0.47 |
0.58 |
0.21 |
0.54 |
0. 64 |
0.36 |
0.35 |
0.95 |
0.14 |
|
Y |
0.41 |
0.54 |
0.51 |
0.37 |
0.31 |
0.23 |
0.56 |
0.89 |
0.17 |
0.03 |
(X是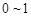 之间的均匀随机数,Y也是
之间的均匀随机数,Y也是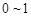 之间的均匀随机数)
之间的均匀随机数)