题目内容
 如图所示,已知矩形ABCD中,AB=
如图所示,已知矩形ABCD中,AB=| 2 |
(1)求证:平面ADC⊥平面BCD;
(2)求点C到平面ABD的距离;
(3)若E为BD中点,求二面角B-AD-C的大小.
分析:(1)由点A在平面BCD上的射影落在DC上,知平面ACD经过平面BCD的垂线,由此能够证明平面ACD⊥平面BCD.
(2)设点C到平面ABD的距离为d,于是VC-ABD=VD-ABC,由DA⊥平面ABC,知DA是三棱锥D-ABC的高,由VC-ABD=VD-ABC,能求出点C到平面ABD的距离.
(3)由ABCD是矩形,知DA⊥AB,BC⊥DC,由平面ACD⊥平面BCD,知BC⊥平面ACD.故BC⊥DA,BC⊥CA,所以DA⊥平面ABC,从面得到∠BAC是二面角B-AD-C的平面角.由此能求出二面角B-AD-C的大小.
(2)设点C到平面ABD的距离为d,于是VC-ABD=VD-ABC,由DA⊥平面ABC,知DA是三棱锥D-ABC的高,由VC-ABD=VD-ABC,能求出点C到平面ABD的距离.
(3)由ABCD是矩形,知DA⊥AB,BC⊥DC,由平面ACD⊥平面BCD,知BC⊥平面ACD.故BC⊥DA,BC⊥CA,所以DA⊥平面ABC,从面得到∠BAC是二面角B-AD-C的平面角.由此能求出二面角B-AD-C的大小.
解答:(1)证明:∵点A在平面BCD上的射影落在DC上,
∴平面ACD经过平面BCD的垂线
∴平面ACD⊥平面BCD.
(2)解:设点C到平面ABD的距离为d,
于是VC-ABD=VD-ABC,
∵ABCD是矩形,
∴DA⊥AB,BC⊥DC,
∵平面ACD⊥平面BCD,
∴BC⊥平面ACD.
∵DA?平面ACD,CA?平面ACD,
∴BC⊥DA,BC⊥CA,
∵AB∩BC=B,
∴DA⊥平面ABC,
∴DA是三棱锥D-ABC的高,
∴由VC-ABD=VD-ABC,
得
dS△ABD=
DAS△ABC,
解得d=
,
即点C到平面ABD的距离为
.
(3)∵DA⊥平面ABC,
∴AC⊥AD,AB⊥AD,
∴∠BAC是二面角B-AD-C的平面角.
在△ABC中,BC=AD=1,AB=
,∠BCA=90°,
∴sin∠BAC=
=
=
,
∴∠BAC=45°.
故二面角B-AD-C是45°.
∴平面ACD经过平面BCD的垂线
∴平面ACD⊥平面BCD.
(2)解:设点C到平面ABD的距离为d,
于是VC-ABD=VD-ABC,
∵ABCD是矩形,
∴DA⊥AB,BC⊥DC,
∵平面ACD⊥平面BCD,
∴BC⊥平面ACD.
∵DA?平面ACD,CA?平面ACD,
∴BC⊥DA,BC⊥CA,
∵AB∩BC=B,
∴DA⊥平面ABC,
∴DA是三棱锥D-ABC的高,
∴由VC-ABD=VD-ABC,
得
| 1 |
| 3 |
| 1 |
| 3 |
解得d=
| ||
| 2 |
即点C到平面ABD的距离为
| ||
| 2 |
(3)∵DA⊥平面ABC,
∴AC⊥AD,AB⊥AD,
∴∠BAC是二面角B-AD-C的平面角.
在△ABC中,BC=AD=1,AB=
| 2 |
∴sin∠BAC=
| BC |
| AB |
| 1 | ||
|
| ||
| 2 |
∴∠BAC=45°.
故二面角B-AD-C是45°.
点评:本题考查平面ADC⊥平面BCD,求点C到平面ABD的距离,求二面角B-AD-C的大小.考查运算求解能力,推理论证能力;考查化归与转化思想.解题时要认真审题,注意把立体问题转化为平面问题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
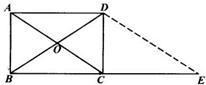 如图所示,已知在矩形ABCD中,
如图所示,已知在矩形ABCD中,
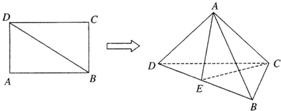 如图所示,已知矩形ABCD中,AB=
如图所示,已知矩形ABCD中,AB= ,AD=1,将△ABD沿BD折起,使点A在平面BCD内的射影落在DC上.
,AD=1,将△ABD沿BD折起,使点A在平面BCD内的射影落在DC上.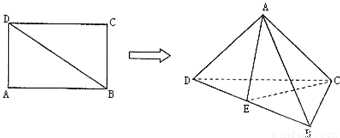 如图所示,已知矩形ABCD中,AB=
如图所示,已知矩形ABCD中,AB=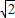 ,AD=1,将△ABD沿BD折起,使点A在平面BCD内的射影落在DC上.
,AD=1,将△ABD沿BD折起,使点A在平面BCD内的射影落在DC上.