题目内容
设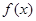 是定义在
是定义在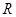 上恒不为零的函数,对任意的实数
上恒不为零的函数,对任意的实数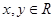 ,都有
,都有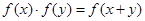 ,若
,若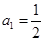 ,
,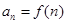 ,(
,(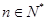 ),则数列
),则数列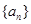 的前
的前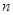 项和
项和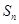 的最小值是( )
的最小值是( )
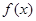 是定义在
是定义在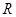 上恒不为零的函数,对任意的实数
上恒不为零的函数,对任意的实数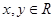 ,都有
,都有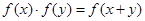 ,若
,若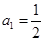 ,
,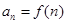 ,(
,(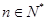 ),则数列
),则数列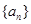 的前
的前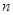 项和
项和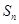 的最小值是( )
的最小值是( )A.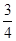 | B.2 | C.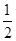 | D.1 |
C
本题考查函数的性质,等比数列的定义和性质及推理能力.
因为,对任意的实数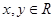 ,都有,且是定义在
,都有,且是定义在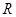 上恒不为零的函数所以
上恒不为零的函数所以
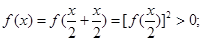 所以
所以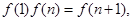 即
即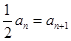 ,所以数列
,所以数列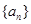 是公比为
是公比为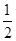 的等比数列,且恒有
的等比数列,且恒有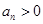 ,则前
,则前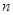 项和
项和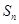 的最小值是
的最小值是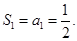 故选C
故选C
因为,对任意的实数
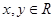 ,都有,且是定义在
,都有,且是定义在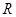 上恒不为零的函数所以
上恒不为零的函数所以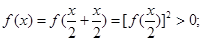 所以
所以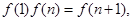 即
即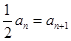 ,所以数列
,所以数列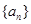 是公比为
是公比为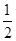 的等比数列,且恒有
的等比数列,且恒有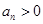 ,则前
,则前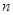 项和
项和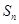 的最小值是
的最小值是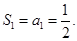 故选C
故选C
练习册系列答案
相关题目
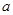 元,每期利率为
元,每期利率为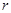 ,设存期为
,设存期为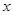 ,本利和(本金加上利息)为
,本利和(本金加上利息)为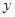 元。
元。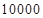 元,每期利率为
元,每期利率为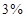 ,试计算
,试计算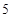 期后的本利和。
期后的本利和。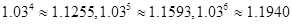 )
)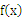 在
在 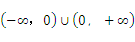 上为奇函数,且
上为奇函数,且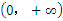 上为增函数,
上为增函数,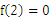 ,则不等式
,则不等式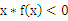 的解集为 _______.
的解集为 _______.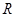 上可导的任意函数
上可导的任意函数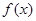 ,若满足
,若满足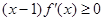 ,则必有( )
,则必有( )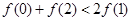



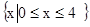 ,Q=
,Q=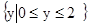 ,则下列对应中不是从P到Q的映射的是( )
,则下列对应中不是从P到Q的映射的是( )



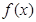 对任意
对任意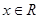 ,都有
,都有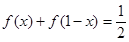 .
.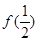 和
和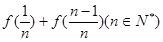 的值;
的值;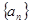 满足:
满足: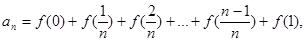 则数列
则数列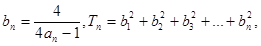
 ,试比较
,试比较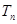 与
与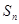 的大小。
的大小。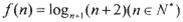 .如果对
.如果对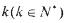 ,满足
,满足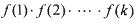 为整数,则称k为“好数”,那么区间[l,2012]内所有的“好数”的和M=________.
为整数,则称k为“好数”,那么区间[l,2012]内所有的“好数”的和M=________.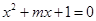 有正根的充要条件是 ( )
有正根的充要条件是 ( )


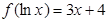 ,则
,则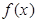 的表达式为( )
的表达式为( )