题目内容
双曲线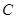 的中心在原点,右焦点为
的中心在原点,右焦点为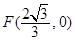 ,渐近线方程为
,渐近线方程为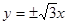 .
.
(Ⅰ)求双曲线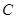 的方程;(Ⅱ)设直线
的方程;(Ⅱ)设直线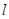 :
: 与双曲线
与双曲线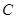 交于
交于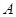 、
、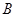 两点,问:当
两点,问:当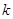 为何值时,以
为何值时,以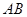 为直径的圆过原点;
为直径的圆过原点;
【答案】
解:(Ⅰ)设双曲线的方程是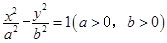 ,则
,则
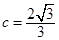 ,
,
又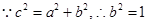 ,
,
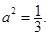
所以双曲线的方程是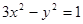 .
.
(Ⅱ)①
由
得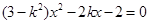 ,
,
由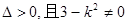 ,得
,得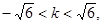 且
且
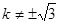 .
.
设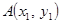 、
、 ,因为以
,因为以 为直径的圆过原点,所以
为直径的圆过原点,所以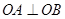 ,
,
所以 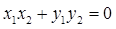 .
.
又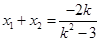 ,
,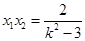 ,
,
所以 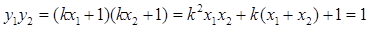 ,
,
所以 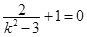 ,解得
,解得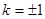 .
.
【解析】略

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
已知双曲线的中心在原点,焦点x轴上,它的一条渐近线与x轴的夹角为α,且
<α<
,则双曲线的离心率的取值范围是( )
| π |
| 4 |
| π |
| 3 |
A、(1,
| ||
B、(
| ||
| C、(1,2) | ||
D、(2,2
|