题目内容
已知双曲线的中心在原点且一个焦点是F(| 7 |
| 2 |
| 3 |
分析:先设出双曲线的方程,然后与直线方程联立方程组,经消元得二元一次方程,再根据韦达定理及MN中点的横坐标可得a、b的一个方程,又双曲线中有c2=a2+b2,则另得a、b的一个方程,最后解a、b的方程组即得双曲线方程.
解答:解:设双曲线方程为
-
=1.
将y=x-1代入
-
=1,整理得(b2-a2)x2+2a2x-a2-a2b2=0.
由韦达定理得x1+x2=
,则
=
=-
.
又c2=a2+b2=7,解得a2=2,b2=5,
所以双曲线的方程是
-
=1.
故答案为:
-
=1.
| x2 |
| a2 |
| y2 |
| b2 |
将y=x-1代入
| x2 |
| a2 |
| y2 |
| b2 |
由韦达定理得x1+x2=
| 2a2 |
| a2-b2 |
| x1+x2 |
| 2 |
| a2 |
| a2-b2 |
| 2 |
| 3 |
又c2=a2+b2=7,解得a2=2,b2=5,
所以双曲线的方程是
| x2 |
| 2 |
| y2 |
| 5 |
故答案为:
| x2 |
| 2 |
| y2 |
| 5 |
点评:本题主要考查代数方法解决几何问题,同时考查双曲线的标准方程与性质等.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 ,0),直线y=x-1与其相交于M,N两点.若MN的中点横坐标为
,0),直线y=x-1与其相交于M,N两点.若MN的中点横坐标为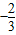 ,则此双曲线的方程为 .
,则此双曲线的方程为 .