题目内容
设函数f(x)=asinωx+bcosωx(ω>0)的定义域为R,最小正周期为π,且对任意实数x,恒有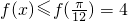 成立.
成立.
(1)求实数a和b的值;
(2)作出函数f(x)在区间(0,π)上的大致图象;
(3)若两相异实数x1、x2∈(0,π),且满足f(x1)=f(x2),求f(x1+x2)的值.
解(1)∵f(x)=asinωx+bcosωx= sin(ωx+φ)(ω>0),
sin(ωx+φ)(ω>0),
又f(x)≤f( )=4恒成立,
)=4恒成立,
∴ =4,即a2+b2=16.…①(1分)
=4,即a2+b2=16.…①(1分)
∵f(x)的最小正周期为π,
∴ω= =2,(2分)
=2,(2分)
即f(x)=asin2x+bcos2x(ω>0).
又f(x)max=f( )=4,
)=4,
∴asin +bcos
+bcos =4,
=4,
即a+ b=8.…②(3分)
b=8.…②(3分)
由①、②解得a=2,b=2 .(4分)
.(4分)
(2)由(1)知f(x)=2sin2x+2 cos2x=4sin(2x+
cos2x=4sin(2x+ ).(5分)
).(5分)
∵0<x<π,
∴ <2x+
<2x+ <
< ,列表如下:(6分)
,列表如下:(6分)
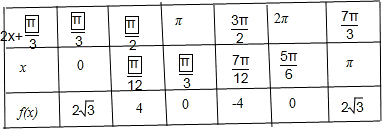
∴函数f(x)的图象如图所示:(8分)
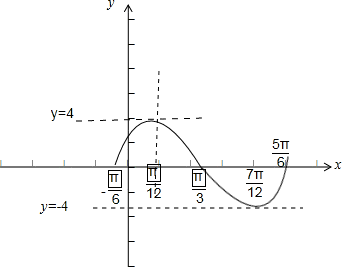
(3)∵f(x1)=f(x2),由(2)知,
当0<x1<x2< 时,x1+x2=2×
时,x1+x2=2× =
= ,(9分)
,(9分)
∴f(x1+x2)=f( )=4
)=4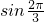 =2
=2 ;…(10分)
;…(10分)
当 <x1<x2<π时,x1+x2=2×
<x1<x2<π时,x1+x2=2× =
= ,(11分)
,(11分)
∴f(x1+x2)=f( )=4sin
)=4sin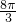 =2
=2 ;…(12分).
;…(12分).
综上,f(x1+x2)=2 .(13分)
.(13分)
分析:(1)将f(x)=asinωx+bcosωx化为;f(x)= sin(ωx+φ),由题意可得
sin(ωx+φ),由题意可得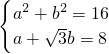 ,从而可求得a和b的值;
,从而可求得a和b的值;
(2)由f(x)=4sin(2x+ )即可做出其大致图象;
)即可做出其大致图象;
(3)当0<x1<x2< 时,x1+x2=
时,x1+x2= ,当
,当 <x1<x2<π时,x1+x2=
<x1<x2<π时,x1+x2= ,从而可求得f(x1+x2)的值.
,从而可求得f(x1+x2)的值.
点评:由y=Asin(ωx+φ)的部分图象确定其解析式,考察两角和与差的正弦,突出五点作图法的考察与应用,综合性强,难度大.
 sin(ωx+φ)(ω>0),
sin(ωx+φ)(ω>0),又f(x)≤f(
 )=4恒成立,
)=4恒成立,∴
 =4,即a2+b2=16.…①(1分)
=4,即a2+b2=16.…①(1分)∵f(x)的最小正周期为π,
∴ω=
 =2,(2分)
=2,(2分)即f(x)=asin2x+bcos2x(ω>0).
又f(x)max=f(
 )=4,
)=4,∴asin
 +bcos
+bcos =4,
=4,即a+
 b=8.…②(3分)
b=8.…②(3分)由①、②解得a=2,b=2
 .(4分)
.(4分)(2)由(1)知f(x)=2sin2x+2
 cos2x=4sin(2x+
cos2x=4sin(2x+ ).(5分)
).(5分)∵0<x<π,
∴
 <2x+
<2x+ <
< ,列表如下:(6分)
,列表如下:(6分)
∴函数f(x)的图象如图所示:(8分)
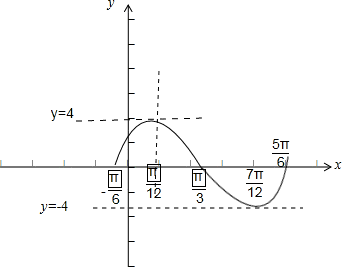
(3)∵f(x1)=f(x2),由(2)知,
当0<x1<x2<
 时,x1+x2=2×
时,x1+x2=2× =
= ,(9分)
,(9分)∴f(x1+x2)=f(
 )=4
)=4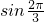 =2
=2 ;…(10分)
;…(10分)当
 <x1<x2<π时,x1+x2=2×
<x1<x2<π时,x1+x2=2× =
= ,(11分)
,(11分)∴f(x1+x2)=f(
 )=4sin
)=4sin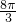 =2
=2 ;…(12分).
;…(12分).综上,f(x1+x2)=2
 .(13分)
.(13分)分析:(1)将f(x)=asinωx+bcosωx化为;f(x)=
 sin(ωx+φ),由题意可得
sin(ωx+φ),由题意可得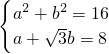 ,从而可求得a和b的值;
,从而可求得a和b的值;(2)由f(x)=4sin(2x+
 )即可做出其大致图象;
)即可做出其大致图象;(3)当0<x1<x2<
 时,x1+x2=
时,x1+x2= ,当
,当 <x1<x2<π时,x1+x2=
<x1<x2<π时,x1+x2= ,从而可求得f(x1+x2)的值.
,从而可求得f(x1+x2)的值.点评:由y=Asin(ωx+φ)的部分图象确定其解析式,考察两角和与差的正弦,突出五点作图法的考察与应用,综合性强,难度大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (n∈N*)
(n∈N*) .
. 对不小于2的正整数恒成立,求x的取值范围.
对不小于2的正整数恒成立,求x的取值范围.