题目内容
13.过坐标原点且与点($\sqrt{3}$,1)的距离都等于1的两条直线的夹角为( )| A. | 90° | B. | 45° | C. | 30° | D. | 60° |
分析 设所求直线方程为kx-y=0,利用点到直线距离公式求出k=0或k=$\sqrt{3}$,由此能求出这两条直线的夹角.
解答 解:当所求直线的斜率不存在时,直线方程为x=0,点($\sqrt{3}$,1)的距离都等于$\sqrt{3}$,不成立;
当所求直线的斜率k存在时,设所求直线方程为y=kx,即kx-y=0,
∵所求直线与点($\sqrt{3}$,1)的距离等于1,
∴$\frac{|\sqrt{3}k-1|}{\sqrt{{k}^{2}+1}}$=1,解得k=0或k=$\sqrt{3}$,
∴这两条直线的夹角为60°.
故选:D.
点评 本题考查两直线夹角的求法,是基础题,解题时要认真审题,注意点到直线距离公式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.若函数f(x)=ax-b的图象如图所示,则( )
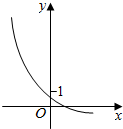

| A. | a>1,b>1 | B. | a>1,0<b<1 | C. | 0<a<1,b>1 | D. | 0<a<1,0<b<1 |
8.“点P(tanα,cosα)在第二象限”是“角α的终边在第四象限”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |