题目内容
设函数y=f(x)的定义域为[a,b],其中b>-a>0,那么F(x)=f(x)+f(-x)的定义域为
- A.[a,-a]
- B.[b,-b]
- C.[a,b]
- D.[b,-a]
A
分析:根据F(x)=f(x)+f(-x)和函数y=f(x)的定义域为[a,b]可得x需满足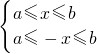 再结合b>-a>0求出x的范围即可得解.
再结合b>-a>0求出x的范围即可得解.
解答:∵函数y=f(x)的定义域为[a,b],F(x)=f(x)+f(-x)
∴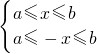
∵b>-a>0
∴a≤x≤b
即F(x)的定义域为[-a,a]
故答案选A
点评:本题主要考查了抽象函数的定义域的求法.解题的关键是要将F(x)=f(x)+f(-x)中的-x看做一个整体在[a,b]的范围内即求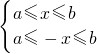 .
.
分析:根据F(x)=f(x)+f(-x)和函数y=f(x)的定义域为[a,b]可得x需满足
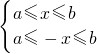 再结合b>-a>0求出x的范围即可得解.
再结合b>-a>0求出x的范围即可得解.解答:∵函数y=f(x)的定义域为[a,b],F(x)=f(x)+f(-x)
∴
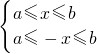
∵b>-a>0
∴a≤x≤b
即F(x)的定义域为[-a,a]
故答案选A
点评:本题主要考查了抽象函数的定义域的求法.解题的关键是要将F(x)=f(x)+f(-x)中的-x看做一个整体在[a,b]的范围内即求
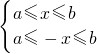 .
. 
练习册系列答案
相关题目