题目内容
12.求函数y=$\sqrt{{x}^{2}-2x+2}+\sqrt{{x}^{2}-4x+13}$的最小值及相应的x值.分析 将函数y变形,可知y的几何意义就是在x轴上的点P(x,0)到A(1,-1)和B(2,3)的距离之和,显然当A、P、B三点共线且P在AB之间时y有最小值,计算即可.
解答 解:∵y=$\sqrt{{x}^{2}-2x+2}+\sqrt{{x}^{2}-4x+13}$
=$\sqrt{(x-1)^{2}+(0+1)^{2}}$+$\sqrt{(x-2)^{2}+(0-3)^{2}}$,
∴y就是在x轴上的点P(x,0)到A(1,-1)和B(2,3)的距离之和,
∴当A、P、B三点共线且P在AB之间时y有最小值,
∵点A、B分别在x轴两侧,
∴只需求出直线AB和x轴的交点即可,
又直线AB方程为:$\frac{y+1}{x-1}=\frac{3+1}{2-1}$,即4x-y-5=0,
令y=0,得x=$\frac{5}{4}$,即点P($\frac{5}{4}$,0)到A(1,-1)和B(2,3)的距离之和最小,
此距离即为AB=$\sqrt{(1-2)^{2}+(-1-3)^{2}}$=$\sqrt{17}$,
即当x=$\frac{5}{4}$时,ymin=$\sqrt{17}$.
点评 本题考查函数表示的几何意义,通过变形建立函数与两点间的距离公式的联系是解题的关键,属于中档题.

练习册系列答案
相关题目
2. 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )| A. | f(x)的图象关于直线$x=-\frac{2π}{3}$对称 | |
| B. | f(x)的图象关于点$(-\frac{5π}{12},0)$对称 | |
| C. | 将函数$y=\sqrt{3}sin2x-cos2x$的图象向左平移$\frac{π}{2}$个单位得到函数f(x)的图象 | |
| D. | 若方程f(x)=m在$[-\frac{π}{2},0]$上有两个不相等的实数根,则m的取值范围是$(-2,-\sqrt{3}]$ |
3.一个频率分布表(样本容量为30)不小心倍损坏了一部分,只记得样本中数据在[20,60)上的频率为0.8,则估计样本在[40,50),[50,60)内的数据个数共为( )


| A. | 15 | B. | 16 | C. | 17 | D. | 19 |
20.已知F是双曲线$\frac{{x_{\;}^2}}{{a_{\;}^2}}-\frac{{y_{\;}^2}}{{b_{\;}^2}}$=1(a>0,b>0)的左焦点,过F作倾斜角为60°的直线l,直线l与双曲线交于点A与y轴交于点B且$\overrightarrow{FA}=\frac{1}{3}\overrightarrow{FB}$,则该双曲线的离心率等于( )
| A. | $\sqrt{5}+1$ | B. | $\frac{{\sqrt{10}+\sqrt{2}}}{2}$ | C. | $\sqrt{5}+1$ | D. | $\frac{\sqrt{7}+1}{2}$ |
4.“a>b”是“3a>3b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
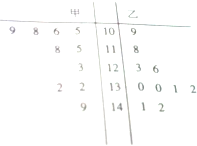 如图记录了甲、乙两名同学其中10次数学成绩.
如图记录了甲、乙两名同学其中10次数学成绩.