题目内容
计算:(1) +
+ +lg20-lg2-(log32)•(log23)
+lg20-lg2-(log32)•(log23)(2)
 -
- -lg
-lg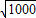 -sin30°+(
-sin30°+( -1)lg1.
-1)lg1.
【答案】分析:(1)利用对数运算性质,以及换底公式和对数恒等式进行化简,即可求出值;
(2)根据根式与分数指数幂的互化和对数运算,以及(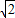 -1)=1,进行化简即可求出所求.
-1)=1,进行化简即可求出所求.
解答:解:(1)原式= +
+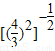 +lg
+lg -
-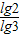 •
•
= +(
+( )-1+lg10-1=
)-1+lg10-1= +
+ +1-1=1…(6分)
+1-1=1…(6分)
(2)原式═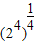 -
-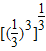 -lg
-lg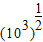 -sin30°+(
-sin30°+(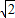 -1)
-1)
=2-( )-1-lg
)-1-lg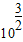 -
- +1=2-3-
+1=2-3- -
- +1=-2…(12分)
+1=-2…(12分)
点评:本题主要考查指数和对数的运算性质,以及根式与分数指数幂的互化及其化简运算,属于基础题.
(2)根据根式与分数指数幂的互化和对数运算,以及(
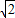 -1)=1,进行化简即可求出所求.
-1)=1,进行化简即可求出所求.解答:解:(1)原式=
 +
+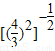 +lg
+lg -
-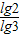 •
•
=
 +(
+( )-1+lg10-1=
)-1+lg10-1= +
+ +1-1=1…(6分)
+1-1=1…(6分)(2)原式═
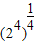 -
-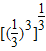 -lg
-lg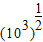 -sin30°+(
-sin30°+(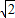 -1)
-1)=2-(
 )-1-lg
)-1-lg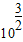 -
- +1=2-3-
+1=2-3- -
- +1=-2…(12分)
+1=-2…(12分)点评:本题主要考查指数和对数的运算性质,以及根式与分数指数幂的互化及其化简运算,属于基础题.

练习册系列答案
相关题目