Question

（2013•济南一模）若双曲线

x2

9

-

y2

16

=1渐近线上的一个动点P总在平面区域（x-m）²+y²≥16内，则实数m的取值范围是

{m|m＞5或m＜-5}

．

Answer 1

分析：求出双曲线的渐近线方程，由题意画出图形，即可求解m的取值范围．

解答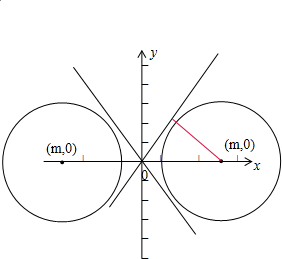：解：双曲线

x2

9

-

y2

16

=1渐近线为：y=±

4

3

x，
因为双曲线

x2

9

-

y2

16

=1渐近线上的一个动点P总在平面区域（x-m）²+y²≥16内，
如图：只需圆心到直线的距离大于半径即可，
圆的圆心坐标（m，0）圆的半径为：4，
所以

|4m|

32+42

＞4，解得：m＞5或m＜-5．
实数m的取值范围是：{m|m＞5或m＜-5}．
故答案为：{m|m＞5或m＜-5}．

点评：本题考查双曲线的简单性质的应用，圆的方程的应用以及线性规划的应用，考查分析问题解决问题的能力．