题目内容

（2013•黄浦区二模）已知点P（x，y）的坐标满足
x-y+1≥0
x+y-3≥0
x≤2
，O为坐标原点，则|PO|的最小值为
3
2
2
3
2
2
．
分析：作出不等式表示的平面区域，明确目标函数的几何意义，利用点到直线的距离公式可得结论．
解答：解：不等式表示的平面区域如图

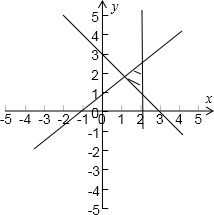
|PO|表示区域内的点与原点的距离，
由点到直线的距离公式可得O到直线x+y-3=0的距离为
3
2
=
3
2
2
，此时由
y=x
x+y-3=0
，可得x=y=
3
2
在区域内
∴|PO|的最小值为
3
2
2

故答案为：
3
2
2
点评：本题考查线性规划知识，考查点到直线的距离公式的运用，考查数形结合的数学思想，属于中档题．
练习册系列答案
相关题目
（2013•黄浦区二模）已知f(x)=4-
1
x
，若存在区间[a，b]⊆(
1
3
，+∞)，使得{y|y=f（x），x⊆[a，b]}=[ma，mb]，则实数m的取值范围是
（3，4）
（3，4）
．
（2013•黄浦区二模）函数f（x）=lg（4-2x）的定义域为
（-∞，2）
（-∞，2）
．
（2013•黄浦区二模）若复数z满足
.
z-1
9z
.
=0，则z的值为
±3i
±3i
．
（2013•黄浦区二模）在正△ABC中，若AB=2，则
AB
•
AC
=
2
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网